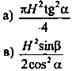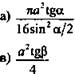Поурочные разработки по Геометрии 11 класс
Зачет по теме: «Тела вращения» - урок 2 - Сфера - ЦИЛИНДР, КОНУС И ШАР
Цель:
- систематизировать знания учащихся;
- обобщить изученный материал.
Ход урока
I. Организационный момент
II. Обобщение и повторение основных моментов теории по теме
1) Поверхность цилиндра состоит из ...
2) Как называется множество точек пространства, находящихся на заданном расстоянии от данной точки?
3) Около всякой ли четырехугольной призмы можно описать цилиндр?
4) Отрезки, соединяющие вершину конуса с точками окружности основания, называют...
5) Перечислите возможное взаимное расположение сферы и плоскости.
6) Точки А и В принадлежат шару. Принадлежит ли этому шару любая точка отрезка АВ?
7) Составьте уравнение сферы с центром в точке А(2; -4; 7) и R = 3.
8) Какая фигура является пересечением сферы х2 + у2 + z2 = 4 и плоскости х + у = 4?
9) Как изменится поверхность шара, если его радиус увеличить в 3 раза?
10) Сколько сфер можно провести через окружность и точку, не лежащую на ней?
11) Плоскость, проходящая через центр шара, называется ...
12) Сечение конуса плоскостью, проходящей через его ось, называется ...
13) Что называется высотой цилиндра?
14) Найдите соответствующую формулу, указав путь стрелкой:

III. Проведение зачета по карточкам (см. приложение)
Ответы:
Уровень |
Вариант |
№ задачи |
Ответ |
II уровень |
2 |
30π см2 |
|
Вариант I |
3 |
36√3 см2 |
|
4 |
8R2 см2 |
||
Вариант II |
2 |
24π см2 |
|
3 |
32π см2 |
||
4 |
а2√2 см2 |
||
Вариант III |
2 |
100π см2 |
|
3 |
36 см2 |
||
4 |
24√3 R2 кв. ед. |
||
Вариант IV |
2 |
42π см2 |
|
3 |
72π см2 |
||
4 |
4πl2/3 кв. ед. |
||
II уровень |
Вариант I |
2 |
4πа(a + b) кв. ед |
3 |
576π см2 |
||
4 |
а) 4R2 sin а/2 tgβ кв. ед. в) 4R2 sin а/2 tgβ кв. ед. |
||
Вариант II |
2 |
па(а + b + 2с) |
|
3 |
7 см |
||
4 |
a) H2ctgβ2 в) H2ctgβ2/cosa |
||
2 |
2пс(а + 2b) |
||
Вариант III |
3 |
|
|
4 |
S sin а/2 |
||
Вариант IV |
2 |
π(ас + 2bс + а2) |
|
3 |
|
||
4 |
|
IV. Подведение итогов
Домашнее задание
I уровень: № 595; 589 а); повт. № 529; 535.
II уровень: № 613; 606; повт. № 529; 535.
I уровень
Карточка № 1
№ 2. Дано: АС = 8 см; ВС = 5 см (рис. 9).
Найти: ОВ.
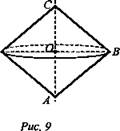
Решение: Sп.п. = 2Sб.п.м. = 2πRl = 2π · OB · ВС. OB = 2п · 3 · 5 = 30π. (Ответ: 30π см2.)
№ 3. Дано: SO = 6 см, ∠SBO = 30° (рис. 10).
Найти: Sсеч.
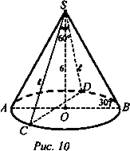
Решение:
![]()
![]() Из ΔSOB: BS = 2SO (так как ∠β = 30°) l = 12 (см).
Из ΔSOB: BS = 2SO (так как ∠β = 30°) l = 12 (см). ![]() (Ответ: 36√3 см2.)
(Ответ: 36√3 см2.)
№ 4. Дано: rшара - R; АС2 = 2х2; АС = х√2 (рис. 11).
Найти. Sп.п.куба.
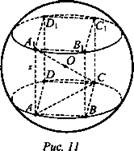
Решение: Sп.п.куба = 6a2. А1С = 2R. Из ΔАА1С ![]() - ребро куба.
- ребро куба. ![]() (кв. ед.). (Ответ: 8R2 кв. ед.)
(кв. ед.). (Ответ: 8R2 кв. ед.)
Карточка № 2
№ 2. Дано: АВ = 4 см; ВС = 3 см (рис. 12).
Найти: Sп.п.
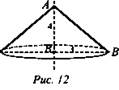
Решение: Sп.п. = πRl + πR2; l = 5 см; R = 3 см. Sп.п. = π · 3 · 5 + π · 32 = 24π (см2). (Ответ: 24π см2..
№ 3. Дано: Rш. = 8 см, ∠OAB = 45° (рис. 13).
Найти: Sceч.
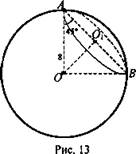
Решение: ![]()
![]() (Ответ: 32π см2.)
(Ответ: 32π см2.)
№ 4. Дано: ABCDA1B1C1D1 - куб (рис. 14).
Найти: Sос.сеч.цил.
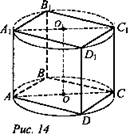
Решение: ![]()
![]() (Ответ: a2√2 кв. ед..
(Ответ: a2√2 кв. ед..
Карточка № 3
№ 2. Дано: AD = 8 см; ВС = 6 см (рис. 15).
Найти: Sп.п.
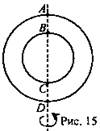
Решение: ![]()
![]() (Ответ: 100π см2)
(Ответ: 100π см2)
№ 3 Дано: ∪CBD = 90°; Hц. = 6 cm; OE = 3 cm (рис. 16).
Найти: Sceч.
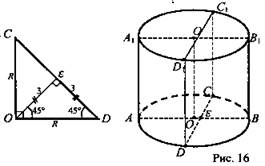
Решение: Sceч. = CD · СС1; Sceч. = 6 · CD; OE = ED = 3 cm; CD = 6 cm; Sceч. = 36 (cm2). (Ответ: 36 см2.)
№ 4. Дано: (рис. 17).
Найти. Sп.п.тетр.
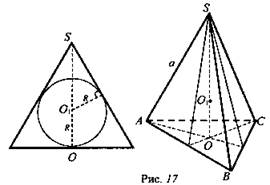
Решение: ![]()
![]() так как
так как ![]()
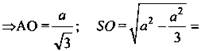
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Карточка № 4
№ 2. Дано: AB = 3 cm; AC = 5 cm (рис. 18).
Найти: Sп.п.
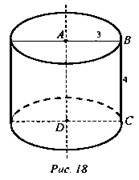
Решение: ![]()
![]() (Ответ: 42π см2.)
(Ответ: 42π см2.)
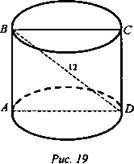
№ 3. Решение: (рис. 19) АВ2 + AD2 = BD2; ![]()
![]() (Ответ: 72π см2.)
(Ответ: 72π см2.)
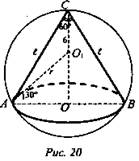
№ 4. Решение: (рис. 20) ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
II уровень
Карточка № 1
№ 2. Дано: ABCD - ромб, АВ = a, BE = b (рис. 21).
Найти: Sп.п.т.вр.
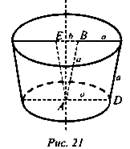
Решение: ![]()
![]()
![]()
![]() (Ответ: 4па(а + b) кв. ед.)
(Ответ: 4па(а + b) кв. ед.)
№ 3. Дано: АВ = 40 см, ОС = 15 см, ОО1 = 7 см. (рис. 22).
Найти: Sсеч.
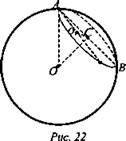
Решение: OO1 ⊥ плоскости сечения. ΔOO1С - прямоугольный: ![]() O1С ⊥ АВ, так как ОС ⊥ АВ и О1С является проекцией наклонной ОС на плоскость сечения. Т. о. из ΔАСО1:
O1С ⊥ АВ, так как ОС ⊥ АВ и О1С является проекцией наклонной ОС на плоскость сечения. Т. о. из ΔАСО1: ![]()
![]() (Ответ: 567п см2.)
(Ответ: 567п см2.)
№ 4 Дано: цилиндр; АВВ1А1 - сечение || оси цилиндра; ∠AOB = α; ∠B1AB = β; АО = ВО = R (рис. 23).
Найти: a) Sсеч. АВВ1А1; б) Sос.сеч. CDD1C.
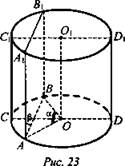
Решение:

![]()
![]()
(Ответ: ![]() )
)
Карточка № 2
№ 2. Дано: AD = а; ВС = b; CD = с (рис. 24).
Найти: Sп.п.т.вр.
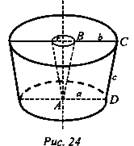
Решение: ![]()
![]()

![]()
(Ответ: ![]() )
)
№ 3 (см. рис. 14) Дано: АВ = 40 см; ОС = 15 см; Sсеч = 576π см2.
Найти: OO1
Решение: πr2 = 576π ⇒ r = 24 (см); т. е. АО1 = 24 см. Из ΔАСО1 (∠ACO1 = 90°): 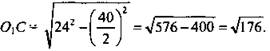 Из ΔОО1С (∠OO1C = 90°);
Из ΔОО1С (∠OO1C = 90°); ![]() (Ответ: 7 см.)
(Ответ: 7 см.)
№ 4. Дано: пл. CDD1C1 || оси цилиндра, ∠DCO = α; ∠D1CD = β; BB1 = H (рис. 25).
Найти: a) Sсеч. CDD1C1; б) Sос.сеч. ABB1A1.
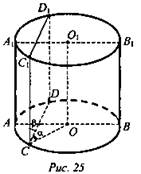
Решение: Из ΔCDD1: ![]()
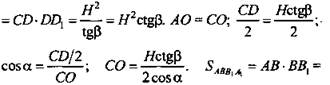
![]() (Ответ:
(Ответ: ![]() )
)
Карточка № 3
№ 2. Дано: ABCD - ромб; AC = а; ВС = с; BE = b (рис. 26).
Найти: Sп.п.т.вр.

Решение: ![]() кв. ед. (Ответ: 2пс(а + 2b) кв. ед.)
кв. ед. (Ответ: 2пс(а + 2b) кв. ед.)
№ 3. Дано: СО = Н; ∠OCB = α; O1С = ОО1; ∠DCE = β (рис. 27).
Найти: Sсеч.окр. (ц. О1; R = A1O1); SDEC.
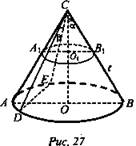
Решение: СО1 = H/2; Из ΔCO1B1: ![]()

![]() (Ответ:
(Ответ: ![]() )
)
№ 4 (см. рис. 8). Дано: цилиндр; ∠COD = α; SADD1A1 = S.
Найти: Sсеч. CDD1C1.
Решение: Sсеч. = CD · DD1; пусть ![]() Из ΔCOD:
Из ΔCOD: ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Карточка № 4
№ 2. Дано: ΔАВС - равнобедренный; АС = а; ВС = с; BE = b (рис. 28).
Найти: Sп.п.т.вр.
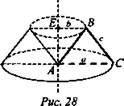
Решение:
![]()
Ответ: п(ас + а2 + 2bс) кв. ед.
№ 3. Дано: конус; CD = a; ∠CSD = β; ∠COD = α (рис. 29).
Найти: a) Sсеч. (О1; R = A1B1); б) Sос.сеч. CDS.
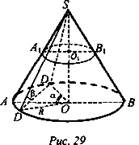
Решение: ![]()
![]()
![]() Из ΔCSK:
Из ΔCSK: ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 4 (см. рис. 29). Дано: цилиндр; SCC1D1D = Q; ∪CBD = α.
Найти: SABB1A1.
Решение: так как ∪CBD = α, то ∠COD = α. Q = CD · DD1; DD1 = Q/CD. Из ΔCOD: ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
IV. Подведение итогов