Зачет по теме: «Тела вращения» - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цель:

- проверка знаний, умений и навыков учащихся при решении задач по теме «Фигуры вращения».

Задачи к зачету (см. приложение.

Ответы:

Уровень	Вариант	№ задачи	Ответ
I уровень	Вариант I	1	36 см2
		2	64π см2
		3	5 м; 12 м
	Вариант II	1	3 дм
		2	18π см
		3	0,5l; 0,25l2√3
II уровень	Вариант I	1	8π см2
		2	36√2 π см2,72 см2
		3	1/8πd2 см2
	Вариант II	1	64π см2
		2	36√2π см2
		3	20 см
III уровень	Вариант I	1	10 см2
		2
		3
	Вариант II	1
		2
		3

II. Домашнее задание

I уровень - № 601, 594; II уровень - № 613; 622.

Решение задач из карточек контрольной работы

II уровень

Вариант I

№ 1. Дано: цилиндр; ABCD - квадрат; АС = 4 см (рис. 1).

Найти: Sб.п.ц.

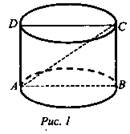
Решение: Sб.п.ц. = 2πRH. Пусть АВ = х, тогда х2 + х2 = 42; 2х2 = 16; х2 = 8; х = 2√2. R = √2; Н = 2√2. Sб.п.ц. = 2π · √2 · 2√2 = 8π (см2). (Ответ: 8π см2.)

№ 2. Дано: конус; АО = ОВ = 6 см; ZSBO = 60°; ZCSD = 45° (рис. 2).

Найти: а) Sсеч.; б) S6.п.конуса.

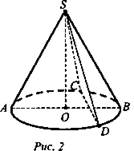
Решение: Так как ∠SBO = 60°, то ∠OSB = 30° ⇒ ОВ = 1/2BS; BS = 12 см, т. е. l = 12 см.

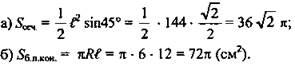
(Ответ: а) 36√2π cм2; б) 72π см2.

№ 3. Дано: шар, AC = d; ∠BAO = 45° (рис. 3).

Найти: Sсеч.

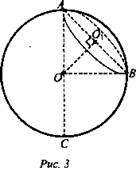
Решение: АО = ОВ = d/2. Из ΔОО1А имеем АO1 = OO1 = х, так как ∠O1AO = 45°, тогда и ∠O1OA = 45°. (Ответ: 1/8πd2 кв. ед.)

Вариант II

№ 1. Дано: цилиндр, ABCD - квадрат; Sосн.ц. = 16π см2 (рис. 4).

Найти: Sб.п.ц.

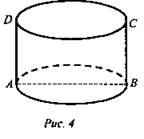
Решение: πR2 = 16π; R2 = 16; R = 4. АВ = ВС = 4 · 2 = 8 (см). Sб.п.ц. = 2πRH, где R = 4; Н = 8. Sб.п.ц. = 2π · 4 · 8 = 64π (см2). (Ответ: 64π см2.)

№ 2. Дано: конус; SO = 6 см; ∠ASB = 90°; ∠CSD = 35° (рис. 5).

Найти: S6.п.конуса.

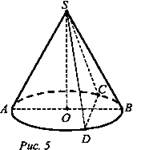
Решение: В ΔASВ, SO - высота и биссектриса, тогда ∠ASO = 45° ⇒ AO = SO. R = H = 6 см. l = 6√2.

(Ответ: 36√2π см2.)

№ 3. Дано: шар, ∠BAO = 30°; Sсеч. = 75π см2 (рис. 6).

Найти: АС.

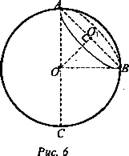
Решение: Из ΔАО1О: (Ответ: 20 см.)

III уровень

Вариант I

№ 1. Дано: шар; Сокр.сеч. = 5π см; ∠BAO = 60° (рис. 7).

Найти: АС.

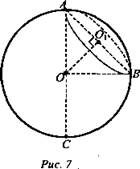
Решение: Из ΔАО1О: (Ответ: 10 см.)

№ 2. Дано: конус; CD = 5 см; ∪CBD = 90°; ∠SEO = 60° (рис. 8).

Найти: Sб.п.к.

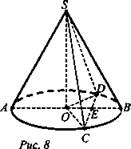
Решение: Sб.п.к. = πRl, так как ∪CBD = 90°, то ∠DOC = 90°. Из ΔDOC: так как ∠SEO = 60°, то ∠ESO = 30° ⇒ OE = 1/2SE. Пусть ОЕ = x; SE = 2х. Из ΔСОЕ: Из ΔСЕО: 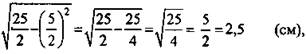тогда SO = 2,5√3 (см). Из ΔSOС: (Ответ: )

№ 3. Дано: цилиндр; ∠КОЕ = α; CD = b; ∪CE1D = β (рис. 9).

Найти: OO1.

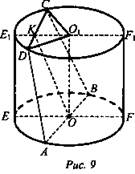
Решение: ∠CO1D = β. Из ΔСO1D: Из ΔО1КС (прямоугольный):

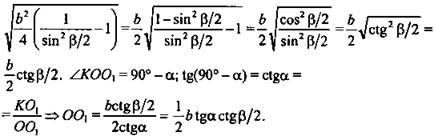
(Ответ: )

Вариант II

№ 1. Дано: шар AC = d; ∠BAC = 30° (рис. 10).

Найти: Сокр.сеч.

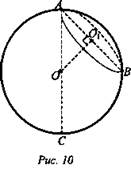
Решение: Сокр.сеч. = 2πr; AO = d/2, так как ∠BAC = 30°, то Из ΔAO1O: (Ответ: )

№ 2. Дано: цилиндр; ∪CBD = 120°; CD1 = 20 см; OK = 3 см (рис. 11).

Найти: Sб.п.ц.

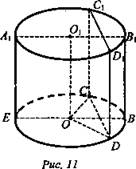
Решение: Sб.п.ц. = 2πRH. ∠COD = 120°; ∠KOD = 60°, тогда ∠KDO = 30° ⇒ OK = 1/2OD. Следовательно, OD = 6 см. Из ΔCDD1: (Ответ: )

№ 3. Дано: конус; АО = ОВ = r; ∠SEO = 60°; ∠SCO = 45° (рис. 12).

Найти: Sceч.

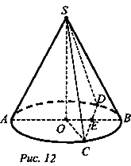
Решение: Из ΔSOC: Из ΔSOE: Пусть OE = x, тогда SE = 2х, так как SO2 + ОЕ2 = SE2, то

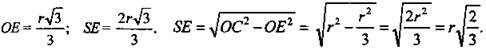
(Ответ: )