Разные задачи на многогранники, цилиндр, конус и шар - урок 3 - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- закрепление знаний, умений и навыков учащихся по изученной теме, устранение пробелов в знаниях;

- совершенствование навыков решения задач по изученной теме.

Ход урока

I. Организационный момент

Учащимся сообщается тема урока.

Формулируются цели урока, виды деятельности учащихся для достижения целей.

II. Тест (см. приложение)

Тест на закрепление теоретических знаний с последующей самопроверкой и обсуждением тех заданий, по которым допущено наибольшие число ошибок.

Учащиеся работают в тетрадях, ответы выписывают на листочках, которые по окончанию работы сдают учителю на проверку. Самопроверка осуществляется по записям в тетрадях.

Учащиеся должны закончить предложенную им фразу, формулирующую понятие.

Ключи к тесту.

Учитель называет правильные ответы, учащиеся сами проверяют свои ответы. Проводится анализ ошибок.

	1	2	3	4	5
Вариант I	б	а	б	а	в
Вариант II	а	б	б	в	в

III. Решение задач

№ 642. По условию задачи используется рис. 157, а) из учебника, предложим решение (рис. 1).

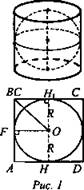
Решение: Рассмотрим осевое сечение. Во всякий цилиндр можно вписать сферу, если его осевое сечение - квадрат. R - радиус сферы, ABCD — квадрат. ВН1 = ОН1 = R, ВН1 - радиус основания цилиндра, НН1 = 2R - высота цилиндра. (Ответ: 2/3.)

№ 643 а). По условию задачи используется рис. 157 б) из учебника, для решения рассмотрим осевое сечение (рис. 2).

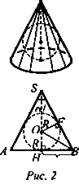
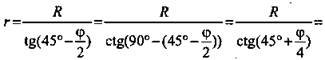
Решение: Высота SH делит осевое сечение на два равных треугольника: SH - биссектриса угла φ. В ΔHBS: ОВ - биссектриса ∠HBS; Из прямоугольного ΔОНВ: (Ответ: )

№ 645. По условию задачи используется рис. 158 а) из учебника, для решения рассмотрим осевое сечение (рис. 3).

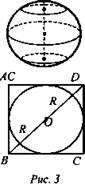
Решение: Около любого цилиндра можно описать сферу. Основание цилиндра является сечениями сферы. Высота цилиндра равна его образующей, а так как образующая равна диаметру основания, то ABCD — квадрат. Примем AD = а, радиус сферы равен R. Из ΔADB: Радиус основания цилиндра a/2. (Ответ: 3/4.)

IV. Подведение итогов

- На последних трех уроках были разобраны задачи на комбинации: сфера и пирамида; сфера и призма; сфера и цилиндр; сфера и конус; цилиндр и призма; конус и пирамида.

- В ходе занятий мы выяснили: всегда ли существует вписанная в многогранник и описанная около многогранника сфера, где находится центр этой сферы.

Домашнее задание

Гл. VI, подготовиться к контрольной работе. Номера: 522, 551 в), 589 а).

Ответы к домашним номерам.

2) если ∠α = 60°;

1)

3) если R = 2 см, α = 30°.