Поурочные разработки по Геометрии 11 класс
Цилиндр. Решение задач - урок 2 - Цилиндр - ЦИЛИНДР, КОНУС И ШАР
Цель урока:
- совершенствовать навыки решения задач по теме.
Ход урока
I. Организационный момент
Сообщение темы и цели урока.
II. Актуализация знаний учащихся
1. Проверить домашнее задание? выписать на доске ответы и указания к задачам из домашней работы, предложить учащимся найти свои ошибки и устранить их. Учитель оказывает индивидуальную помощь при необходимости.
2. Разобрать задачу, с которой не справилось большинство учащихся.
III. Повторение изученных на предыдущих уроках формул в ходе решения зада.
№ 541 (рис. 1).
Решение:
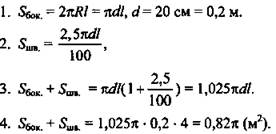
(Ответ: 0,82π м2.)
№ 545 (рис. 2).
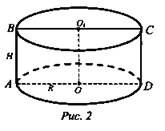
Решение: АВO1O - квадрат со стороной а.
а) сечение - прямоугольник ABCD; ![]()
![]()
![]()
Дополнительная задач.
№ 540 (рис. 3).
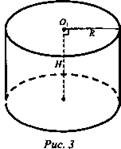
Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см2. Найдите радиус основания и высоту цилиндра.
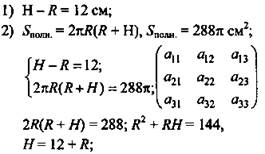
![]()
![]() не удовлетворяет условию R > 0;
не удовлетворяет условию R > 0; ![]()
4) R = 6 см; Н = 12 + 6 = 18(см).
(Ответ: 6 см; 18 см.)
IV. Самостоятельная работа (см. приложение).
Решение задач самостоятельной работы
I уровень
Вариант I
1. (рис. 4).
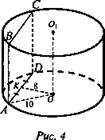
1) ABCD - квадрат.
2) АО = 10 см, ОК = 8 см. OK ⊥ AD, АК = KD.
3) ΔАКО прямоугольный. ![]()
![]()
4) AD = 6 · 2 = 12 (см).
5) SABCD = 122 = 144 (см2).
(Ответ: 144 см2.)
2. (рис. 5).
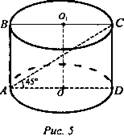
1) ABCD - осевое сечение.
2) АС = 8√2 дм, ΔACD - прямоугольный, AD = DC, 2AD2 = AC2, AD = 8 (дм).
3) AD = CD = Н = 8 (дм).
4) ![]()
![]()
(Ответ: 96п дм2.)
Вариант II
1. (рис. 6).
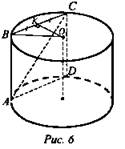
1) ABCD - квадрат.
2) ОО1 = АВ = 16 см, KО1 = 6см, так как КО1 расстояние от ОО1 до ABCD, К - середина ВС.
3) ВС = 16 см ⇒ ВК = 8 см.
4). ΔВКО1 - прямоугольный. ![]()
![]()
(Ответ: 10 см.)
2. (рис. 7).
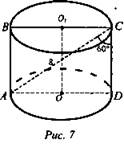
1) ΔACD - прямоугольный, ∠ACD = 60° ⇒ ∠CAD = 30°.
2) Так как ∠CAD = 30°, то CD = 1/2AC, CD = 4 см = H.
3) ![]()
4) ![]()
![]()
(Ответ: ![]() )
)
II уровень
Вариант I
1. (рис. 8).
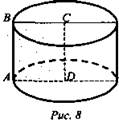
1) ABCD - прямоугольник, CD = 5 см.
2) Sбок. = 100π см2, Sбок. = 2πR · h, 100π = 2πR · 5, R = 10 см, AD = 10 см.
3) Sabcd = АВ · AD, Sabcd = 5 · 10 = 50 см2.
(Ответ: 50 см2.)
2. (рис. 9).
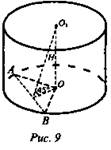
1) ∪ АВ = 120° ⇒ ∠AOB = 120° (центральный).
2) ΔKOO1 - равнобедренный, так как ∠O1KO = 45° ⇒ КО = OO1 = 4 см.
3) ΔЛОВ - равнобедренный, так как АО = ОВ = R, OK ⊥ АВ (по свойству медианы).
4) ∠OAB = 30° ⇒ АО = 2ОК; АО = 8 см, R = 8 см.
5) Sсеч. = 2R · ОО1, Sсеч. = 16 · 4 = 64 (см2).
(Ответ: 64 см2.)
Вариант II
1.
1) Sбок. = 60π см2, Sбок. = 2πRH, 60π = 2πRH, 30 = RH.
2) По условию R = 5 см ⇒ H = 30/5 = 6 (см).
3) S= 5 · 6 = 30 (см2).
(Ответ: 30 см2.)
2. (рис. 10).
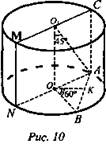
1. Sосн.сеч. = SANMС = ОО1 · 2АО.
2. Так как ∠AO1O = 45° ⇒ ΔАОО1 - равнобедренный, прямоугольный, значит, АО = ОО1.
3. ![]() (OK ⊥ АВ, BK = KA).
(OK ⊥ АВ, BK = KA).
4. ОО1 = 4 см, NA = 20A = 2 · 4 = 8 (см). Sсеч. = 4 · 8 = 32 (см2).
(Ответ: 32 см2.)
III уровень
Вариант .
1. (рис. 11).
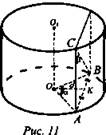
1) ΔАВО - равнобедренный, так как АО = ОВ = R ⇒ ![]()
2) ΔАОК - прямоугольный, 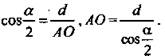

2. (рис. 12).
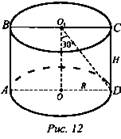
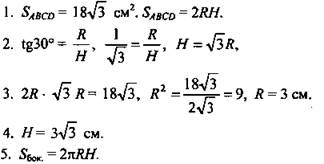
![]()
(Ответ: ![]() )
)
III уровень
Вариант II
1. (рис. 13).
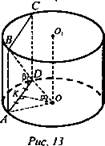
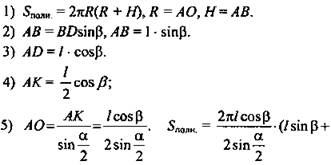
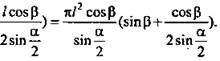
(Ответ: ![]() )
)
2. (рис. 14).
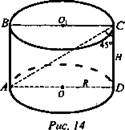

(Ответ: 81π см2.)
V. Подведение итогов
- На этом уроке мы повторили формулы, изученные на предыдущих уроках, и применили эти формулы в решении задач при выполнении самостоятельной работы.
Домашнее задание
а) Повторить п. 53, 54. б) № 539, 538, 535.
№ 538 (рис. 15).
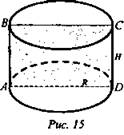

(Ответ: S/π.)
№ 539 (рис. 16).
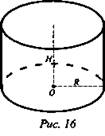

2) Краска: 0,2 · 5,0625π = 1,0125π (кг) ≈ 3,18 кг.
(Ответ: 3,18 кг.)
№ 535 (рис. 17).
1) OK ⊥ АВ;
2) Так как ΔAОВ равнобедренный, то К — середина АВ;

5) ABCD - прямоугольник (сечение). ![]()
![]()
(Ответ: 40 см2.)