Конус - Конус - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- формирование понятий конической поверхности, конуса;

- умение работать с рисунком и читать его;

- применение знаний в решении задач.

Ход урока

I. Организационный момент

Сообщение темы урока, цепей урока.

- Сдайте тетради с домашней работой. Приготовьте необходимые принадлежности: тетрадь по теории, рабочие тетради, ручку, карандаш, резинку.

II. Объяснение новой темы

- Сегодня мы рассматриваем пространственную геометрическую фигуру - «круглое», геометрическое тело - конус (показать макет конуса).

1) Рассмотрим рисунок (готовый рисунок на доске).

На плоскости рассмотрим окружность с центром в точке О и прямую ОР, перпендикулярную к плоскости этой окружности. Соединим отрезком точку Р с каждой точкой окружности. Поверхность, образованная этими отрезками, называется конической поверхностью, а эти отрезки - образующими конической поверхности.

2) А теперь запишем определения новых понятий в тетрадях по теории и построим чертеж конуса.

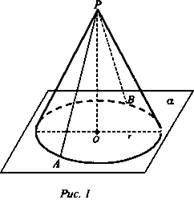
Конической поверхностью называется поверхность, образованная отрезками, соединяющими каждую точку окружности с точкой перпендикуляра, проведенного к плоскости окружности через ее центр. Эти отрезки называются образующими конической поверхности.

3) Изображение конуса на чертеже:

Комментарий учителя к построению: изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения. Обычно выбирается то из них, которое создает правильное представление о форме фигуры и наиболее удобно для исследования ее свойств. Здесь, граница круга - окружность - изображается на плоскости эллипсом.

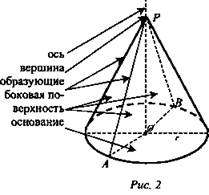
4) Тело, ограниченное конической поверхностью и кругом, называется конусом. Коническая поверхность называется боковой поверхностью конуса. Круг - основанием конуса.

Точка перпендикуляра к плоскости основания, проведенного через центр круга, называется вершиной конуса (на чертеже - точка Р).

Образующие конической поверхности - образующими конуса. Прямая, проходящая через центр основания и вершину, называется осью конуса. Отрезок, соединяющий вершину конуса с центром круга, называется высотой конуса.

III. Устные задачи - чтение графика - отработка нового материала

1) Назвать две образующие конуса, сравнить их. Сделать вывод. (Добиться от учеников вывода равенства двух образующих конуса.)

2) Назвать углы наклона образующих конуса к плоскости основания, сравнить их. (Доказательство равенства углов.)

3) Каков угол между осью конуса и основанием. Почему?

4) Каков вид треугольника АОР?

5) Что за фигура образуется вращением прямоугольного треугольника относительно одного из катетов? (Показать наглядно, что получается.) В условии 1 вопроса, уточним: что образуется вращением гипотенузы? (Боковая поверхность конуса.) Что образуется вращением катета? (Основание.)

6) Каким способом можно получить конус?

IV. Сечение конуса (Изучение новой темы по готовым чертежам)

Учитель дает определения сечениям. Ученики записывают. По наводящим вопросам учителя ученики должны сказать, что представляет собой данное сечение и его основные свойства.

1) Сечение, проходящее через ось конуса, называется осевым.

Вопросы: какую фигуру представляет это сечение? (равнобедренный треугольник).

Основание которого - диаметр основания конуса.

Боковые стороны — образующие конуса.

Высота треугольника - высота конуса.

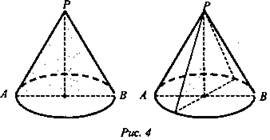
2) Сечение, проходящее через вершину конуса, но не ось, - треугольник. Вопросы: вид треугольника. Чем являются боковые стороны?

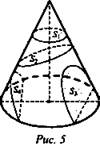
3) Сечение, перпендикулярное оси конуса, - круг. (S1) Вопросы: как найти коэффициент подобия сечения и основания? Как по радиусу основания найти радиус сечения?

4) Сечение плоскостью, пересекающей все образующие, - эллипс. (S2)

5) Сечение плоскостью, параллельной двум образующим конуса, - гипербола (S3).

6) Сечение плоскостью, параллельной одной образующей, - парабола (S4). В школьном курсе часто применяются: осевое сечение и сечение, параллельное основанию.

V. Историческая справка

Исторически появление эллипса, параболы и гиперболы связано с изучением конических сечений математиками Древней Греции. Основной труд Апполония Пергского так и назывался - «Конические сечения» (III век до н.э.). Эти кривые интересны еще и тем, что траектория движения небесных тел происходит по одной из этих кривых. Это так же траектория движения космических ракет.

VI. Развертка конуса (рис. 6)

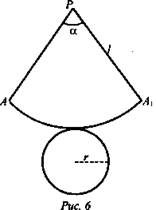
1) Боковую поверхность конуса развернем на плоскость, разрезав ее по одной из образующих. Образуется круговой сектор, у которого радиусом является образующая конуса, а длина дуги сектора - длина окружности основания конуса.

2) За площадь боковой поверхности конуса принимается площадь ее развертки. Площадь кругового сектора равна где α - градусная мера дуги АРА1; l - образующая, r-радиус основания.

Выразим α через l и r. Длина дуги развертки равна длине дуги конуса окружности. откуда Подставив в первоначальную формулу, получим:

Итак, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

3) Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

VII. Формирование умений и навыков учащихс.

Задача № 547.

Дано: конус, ОР = 15 см, ОВ = r = 8 см (рис. 7).

Найти: РВ.

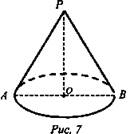
Решение: Из ΔОРВ по теореме Пифагора; (Ответ: 17 см.)

Задача № 549 а).

Дано: конус. О2Р = 8 дм. (рис. 8).

Найти: О1Р.

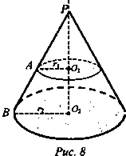
Решение: Сечение и основание конуса – круги - подобны. Площади подобных фигур относятся как квадрат коэффициента подобия. Пусть РО1 = X дм, тогда PO1 - искомый отрезок. (Ответ: 4√2 дм.)

VIII. Подведение итогов

Вопросы:

1) Объясните, какое тело называется конусом?

2) Что такое образующая конуса?

3) Радиус основания конуса 3 см, высота 4 см. Найти образующую. (Ответ: 5 см.)

Домашнее задание

П. 55, 56, № 548, 549 б), 550.