Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Зачетная работа по теме «Уравнения и неравенства с двумя переменными» - Неравенства с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Цель: проверка знаний учащихся по вариантам одинаковой сложности.
Ход урока
I. Сообщение темы и цели урока
II. Варианты зачетной работы
Вариант .
А
1. Решите систему уравнений.

2. Даша и Таня пропалывают грядку за 12 мин, а одна Даша - за 20 мин. За сколько минут пропалывает грядку одна Таня?
3. Изобразите на координатной плоскости множество решений:
а) уравнения 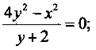
б) неравенства (у - 1)(у - х) ≤ 0;
в) системы неравенств 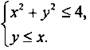
4. Решите систему уравнений 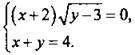
В
5. Решите систему уравнений.
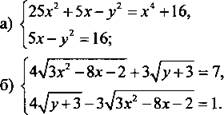
6. Семья состоит из двух человек: мужа и жены. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 60%. На сколько процентов вырос бы общий доход семьи, если бы вдвое увеличилась зарплата жены?
7. На координатной плоскости изобразите множество решений неравенства ![]()
С
8. Решите систему уравнений.

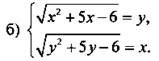
9. Найдите значение параметра, при котором система уравнений 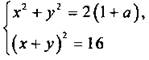 имеет ровно два решения. Найдите эти решения.
имеет ровно два решения. Найдите эти решения.
Вариант .
А
1. Решите систему уравнений.

2. Олег и Витя вскапывают грядку за 10 мин, а один Олег – за 15 мин. За сколько минут вскапывает грядку один Витя?
3. Изобразите на координатной плоскости множество решений:
а) уравнения ![]()
б) неравенства (х + 1)(у + х) ≤ 0;
в) системы неравенств 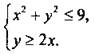
4. Решите систему уравнении 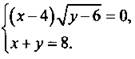
В
5. Решите систему уравнений.

6. Семья состоит из двух человек: мужа и жены. Если бы зарплата жены увеличилась вдвое, общий доход семьи вырос бы на 45%. На сколько процентов вырос бы общий доход семьи, если бы вдвое увеличилась зарплата мужа?
7. На координатной плоскости изобразите множество решений неравенства ![]()
С
8. Решите систему уравнений.
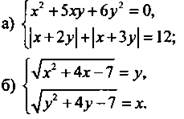
9. Найдите значение параметра, при котором система уравнений  имеет ровно два решения. Найдите эти решения.
имеет ровно два решения. Найдите эти решения.
III. Ответы и решени.
Вариант 1
1. Ответ: а) (1; 1), (1; -2), (3,5; 4); б) (1/3; -1/2).
2. Ответ: 30 мин.
3. Ответ: a-в) построено.
4. Ответ: (1; 3).
5. Ответ: а) (5; 3), (5; -3); б) (3; -2), (-1/3; -2).
6. Ответ: на 40%.
7. Ответ: построено.
8(a). Для решения системы уравнений  запишем ее в виде
запишем ее в виде  Так как в первом уравнении произведение множителей равно нулю, то один из них равен нулю. Получаем две системы уравнений:
Так как в первом уравнении произведение множителей равно нулю, то один из них равен нулю. Получаем две системы уравнений:
 откуда х = 4, у = -4 и х = -4, у = 4;
откуда х = 4, у = -4 и х = -4, у = 4;
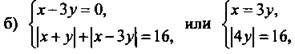 откуда х = 12, у = 4 и х = -12, у = -4.
откуда х = 12, у = 4 и х = -12, у = -4.
Ответ: (4; -4), (-4; 4), (12; 4), (-12; -4).
8(б). Для системы уравнений  учтем, что х, у ≥ 0, и возведем в квадрат уравнения
учтем, что х, у ≥ 0, и возведем в квадрат уравнения 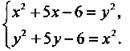 Вычтем уравнения системы и получим: х2 - у2 + 5х – 5y = у2 - х2, или 2(х – y)(x + y) + 5(х - y) = 0, или (х - у)(2х + 2у + 5) = 0. Так как х, у ≥ 0, то в произведении только первый множитель равен нулю, т. е. у = х. Подставим это значение в первое уравнение: х2 + 5х - 6 = х2, откуда 5х - 6 = 0 и х = 1,2, у = 1,2.
Вычтем уравнения системы и получим: х2 - у2 + 5х – 5y = у2 - х2, или 2(х – y)(x + y) + 5(х - y) = 0, или (х - у)(2х + 2у + 5) = 0. Так как х, у ≥ 0, то в произведении только первый множитель равен нулю, т. е. у = х. Подставим это значение в первое уравнение: х2 + 5х - 6 = х2, откуда 5х - 6 = 0 и х = 1,2, у = 1,2.
Ответ: (1,2; 1,2).
9. Удобнее всего исследовать систему уравнений 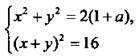 графически. Графиком первого уравнения является окружность с центром в начале координат и радиусом
графически. Графиком первого уравнения является окружность с центром в начале координат и радиусом ![]() Графиком второго уравнения будут две параллельные прямые: х + у = ±4 или у = -х ± 4. Очевидно, что данная система будет иметь ровно два решения, если построенные прямые будут касаться окружности. Из прямоугольного равнобедренного треугольника ОАВ получаем условие:
Графиком второго уравнения будут две параллельные прямые: х + у = ±4 или у = -х ± 4. Очевидно, что данная система будет иметь ровно два решения, если построенные прямые будут касаться окружности. Из прямоугольного равнобедренного треугольника ОАВ получаем условие: ![]() или
или ![]() или 4 = 1 + а, откуда а = 3. Легко найти решения системы, т. е. координаты точек касания А и Д: (2; 2) и (-2; -2).
или 4 = 1 + а, откуда а = 3. Легко найти решения системы, т. е. координаты точек касания А и Д: (2; 2) и (-2; -2).

Ответ: при a = 3 (2; 2) и (-2; -2).
Вариант 2
1. Ответ: а) (-2; 4), (-3; 1), (4; 1); б) (-1/4; 1/2).
2. Ответ: 30 мин.
3. Ответ: a-в) построено.
4. Ответ: (2; 6).
5. Ответ: а) (4; 2), (4; -2); б) (2; 3), (4/3; 3).
6. Ответ: на 55%.
7. Ответ: построено.
8(a). Для решения системы уравнений 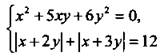 запишем ее в виде
запишем ее в виде 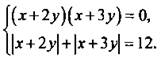 Так как в первом уравнении произведение множителей равно нулю, то один из них равен нулю. Получаем две системы уравнений:
Так как в первом уравнении произведение множителей равно нулю, то один из них равен нулю. Получаем две системы уравнений:
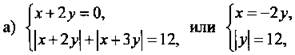 откуда х = 24, у = -12 и х = -24, у = 12;
откуда х = 24, у = -12 и х = -24, у = 12;
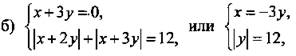 откуда х = 36, у = -12 и х = -36, у = 12.
откуда х = 36, у = -12 и х = -36, у = 12.
Ответ: (24; -12), (-24; 12), (36; -12), (-36; 12).
8(б). Для системы уравнений 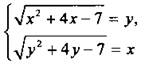 учтем, что х, у ≥ 0, и возведем в квадрат уравнения
учтем, что х, у ≥ 0, и возведем в квадрат уравнения 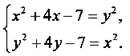 Вычтем уравнения системы и получим: х2 - у2 + 4х - 4у = у2 - х2, или 2(х - y)(х + y) +4(х - у) = 0, или (х - у)(х + у + 2) = 0. Так как х, у ≥ 0, то в произведении только первый множитель равен нулю, т. е. у = х. Подставим это значение в первое уравнение: х2 + 4х - 7 = х2, откуда 4х - 7 = 0 и х = 7/4, у = 7/4.
Вычтем уравнения системы и получим: х2 - у2 + 4х - 4у = у2 - х2, или 2(х - y)(х + y) +4(х - у) = 0, или (х - у)(х + у + 2) = 0. Так как х, у ≥ 0, то в произведении только первый множитель равен нулю, т. е. у = х. Подставим это значение в первое уравнение: х2 + 4х - 7 = х2, откуда 4х - 7 = 0 и х = 7/4, у = 7/4.
Ответ: (7/4; 7/4).
9. Удобнее всего исследовать систему уравнений  графически. Графиком первого уравнения является окружность с центром в начале координат и радиусом
графически. Графиком первого уравнения является окружность с центром в начале координат и радиусом ![]() Графиком второго уравнения будут две параллельные прямые: у - х = ±2 или у = х ± 2. Очевидно, что данная система будет иметь ровно два решения, если построенные прямые будут касаться окружности. Из прямоугольного равнобедренного треугольника ОАВ получаем условие:
Графиком второго уравнения будут две параллельные прямые: у - х = ±2 или у = х ± 2. Очевидно, что данная система будет иметь ровно два решения, если построенные прямые будут касаться окружности. Из прямоугольного равнобедренного треугольника ОАВ получаем условие: ![]() или
или ![]() или 1 = 1 - а, откуда а = 0. Легко найти решения системы, т. е. координаты точек касания А и Д: (-1; 1) и (1; -1).
или 1 = 1 - а, откуда а = 0. Легко найти решения системы, т. е. координаты точек касания А и Д: (-1; 1) и (1; -1).
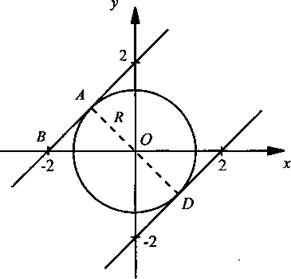
Ответ: при а = 0 (-1; 1) и (1; -1).