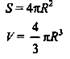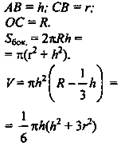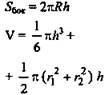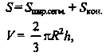Поурочные разработки по Геометрии 11 класс
Повторение по теме: «Тела вращения» - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цели урока:
- систематизировать теоретические знания по теме «Тема вращения»;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщаем тему, формулируем цель урока.
Проверка домашнего задания через кодоскоп (взаимопроверка).
II. Актуализация знаний учащихся
Повторение теоретических сведений с помощью таблицы.
Цилиндр |
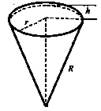
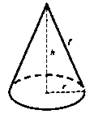
Конус |
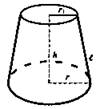
Усеченный конус |
|||
|
|
|
|||
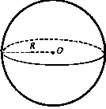
Шар |
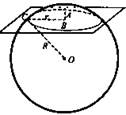
Шаровой сегмент |
Шаровой слой |
Шаровой сектор |
||
|
|
|
где h - высота сегмента, содержащегося в секторе. |
||
III. Тест с последующей проверкой по кодоскопу (см. приложение.
Ответы:
Вариант I: а); б); в); г); а); в); а);
Вариант II: в); в); б); а); б); в); в).
I уровень №1-4;
II уровень № 1-6;
III уровень № 1-7.
IV. Решение задач по готовым чертежам
Осевое сечение цилиндра - квадрат, диагональ которого равна 20 см. Найдите высоту цилиндра, площадь основания, площадь боковой поверхности (рис. 1).
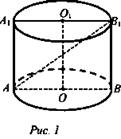
Решение: АА1В1В - квадрат. ![]()
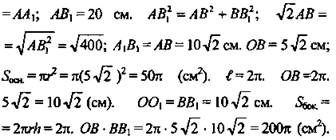
(Ответ: ![]() )
)
2) Дано: ΔCDE - правильный. SO - высота конуса (рис. 2).
Найти: объем и площадь боковой поверхности конуса.
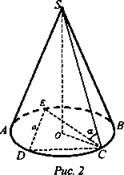
Указание: ![]() Из ΔECS:
Из ΔECS: ![]() Из ΔSOC:
Из ΔSOC: ![]() (Ответ:
(Ответ: 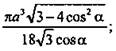
![]() )
)
3) О и O1 - центры оснований усеченного конуса. Найти объем и площадь боковой поверхности конуса (рис. 3).
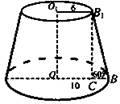
Рис. 3
Указание: проведем В1С ⊥ OВ. CB = 4 см. Из ΔB1CB: ![]() (Ответ:
(Ответ: ![]() )
)
4) О - центр шара, O1 - центр круга - сечения шара плоскостью, α = 60° (рис. 4).
Найти: площадь сечения шара плоскостью, объем и площадь поверхности шара.
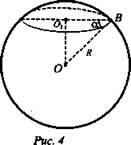
Решение: ![]()

(Ответ: ![]() )
)
V. Самостоятельная работа
№ 1. Радиусы окружностей, являющихся сечениями сферы двумя параллельными плоскостями, равны 3 см и 4 см, а расстояние между этими плоскостями равно 7 см. Найдите площадь сферы.
Дано: O1А = 3 см; ОВ = 4 см; OO1 = 7 см (рис. 5).
Наити: Sсферы.
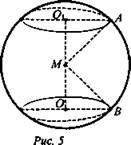
Решение: ОМ = х.
Из 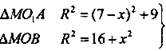 по теореме Пифагора.
по теореме Пифагора. ![]()
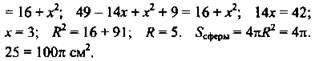
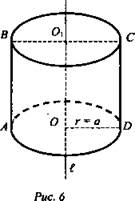
№ 2. Квадрат со стороной а вращается вокруг прямой, проходящей через его сторону. Найдите: I уровень - площадь осевого сечения, полученного цилиндра; II уровень - площадь боковой поверхности этого цилиндра; III уровень - площадь полной поверхности полученного цилиндра.
Дано: OO1 = O1С = CD = OD = а (рис. 6).
Найти: Sполн., Sбок., Sсеч..
Решение: ![]() (Ответ: 2а2..
(Ответ: 2а2..
![]() (Ответ: 2πа2.)
(Ответ: 2πа2.)
![]()
№ 3. Длина образующей конуса 2√3, а угол при вершине осевого сечения конуса равен 120° (рис. 7).
Найдите: I уровень – Sосн.; II уровень - Sбок.; III уровень - Sполн.
Дано: ∠ASB = 120°; AS = 2√3 см (рис. 7).
Найти: 1) Sосн.; 2) Sбок.; 3) Sполн.
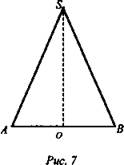
Решение: SO ⊥ AB; AO = OB; ΔAOS; ∠ASB = ∠OSB = 60°. ![]()

№ 4. Отрезок AВ - хорда основания конуса, которая удалена от оси на 3 см. МO - высота конуса, причем МО = 6√2 см, где М - вершина конуса. Найдите расстояние от точки О до плоскости, проходящей через точки А, В и М.
Дано: АВ - хорда, ОК = 3 см; МО - высота конуса; МО = 6√2 см (рис. 8).
Найти: OD.
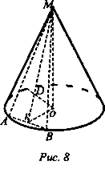
Решение: ΔКМО; ОМ ⊥ OК. По теореме Пифагор.

(Ответ: 2√2 см.)
Домашнее задание
Тест в 4-х вариантах (см. приложение.
Ответы:
Вариант I: г); б); а); г); а); в); а).
Вариант II: в); б); в); в); б); в); б).
Вариант III: в); а); в); а); а); б); в).
Вариант IV: а); б); в); б); б); а); а).
I уровень № 1-4; II уровень № 1-7.
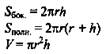
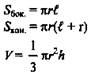
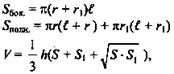 где S и S1 - площади оснований
где S и S1 - площади оснований