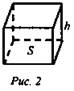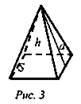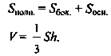Поурочные разработки по Геометрии 11 класс
Повторение по теме: «Многогранники» - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цель урока:
- систематизировать теоретические знания по теме «Многогранники»;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщаем тему, формулируем цель урока.
II. Актуализация знаний учащихся
1. Повторение теоретических сведений с помощью таблицы.
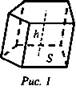
Призма
|
Прямая призма
|
Пирамида
Правильная пирамида.
a - апофема |
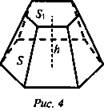
Усеченная пирамида
Правильная усеченная пирамида.
|
III. Тест с последующей проверкой (см. приложение)
Ответы:
Вариант I: б); в); а); в); а); а); б).
Вариант II: в); б); б); в); а); а).
I уровень решают № 1-4;
II уровень решают № 1-6;
III уровень решают № 1-7.
Учащиеся решают задачи самостоятельно, записывая краткое решение в тетрадях.
Проверка правильности выполнения теста производится с помощью кодоскопа. Учащиеся в парах меняются тетрадями и проверяют друг друга.
За решение задач № 1-4 ставится отметка «3»; № 1-6 - «4»; № 1-7 - «5».
IV. Решение задач по готовым чертежам
Учащиеся решают задачи самостоятельно, записывая кратко решение в тетрадях, затем один из учащихся выходит к доске и рассказывает решение задачи.
Остальные проверяют правильность своего решения.
№ 1. Дано: Sполн. = 378; А1В1 = 14; В1С1 = 15; A1C1 = 13 (рис. 5).
Найти: АА1, Sполн., Sбок., V.
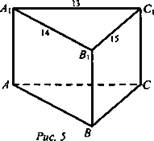
Решение: ΔABC = ΔA1B1C1; ![]()
![]()
![]()
(Ответ: 5; 378; 210; 420.)
№ 2. Дано: А2А4' = 12; ∠A4A2A4' = 30°. А1А2А3А4А1'А2'А3'А4' - правильная призма (рис. 6).
Найти: Sполн., Sбок., V.
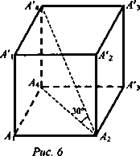
Решение: ![]()
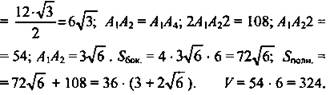
(Ответ: ![]() )
)
№ 3. Дано: SO = 4 - высота пирамиды. ABCD - прямоугольник, AD = ВС = 6; AВ = DC = 8 (рис. 7).
Найти: Sполн., Sбок., V.
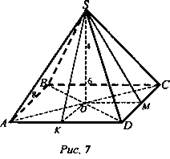
Решение: ![]()
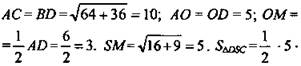
![]() (средняя линия ΔADC). OK = 4.
(средняя линия ΔADC). OK = 4. ![]()
![]()
![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Самостоятельная работа (см. приложение)
Ответы: I уровень: ![]() II уровень а3; III уровень 2а3.
II уровень а3; III уровень 2а3.
Решение самостоятельной работ.
I уровень
Дано: SABCD - пирамида. АВ = ВС = DC = AD = a. SB ⊥ пл. ABCD (рис. 8). SP = PC. ∠POM = α.
Найти: V.
Решение: Проведем ОМ || АВ; ОМ = a/2; РМ из ΔОРМ. РМ = ОМtgα. МР - средняя линия в ΔSBC.
![]()
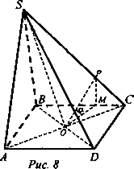
На ребрах AD, CC1 и A1B1 правильной призмы ABCDA1B1C1D1 взяты соответственно точки Р, Q, R - середины этих ребер. Найдите объем призмы, если AD = а и о треугольнике PQR известно, что он:
II уровень - равносторонний.
III уровень - прямоугольный.
Дано: правильная призма. A1R = RB1, C1Q = QC; AP = PD. АВ = ВС = CD = AD = а; 1) RP = PQ = RQ. 2) ΔRQP – прямоугольный (рис. 9).
Найти: V.
Решение:
1) В ΔABD РК - средняя линия. ![]()
![]() (Из ΔKRP).
(Из ΔKRP). ![]() (Из ΔPCD).
(Из ΔPCD). ![]()
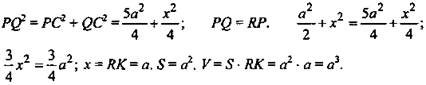
2) PQ = RQ, так проекции ![]() ΔRQP - равнобедренный прямоугольный.
ΔRQP - равнобедренный прямоугольный. ![]() RP2 из ΔPRO.
RP2 из ΔPRO.
![]()
![]()
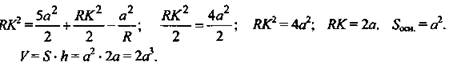
V. Подведение итогов
Вопросы:
- Какие теоретические вопросы мы повторили?
- По каким формулам вычисляют площади боковой и полной поверхности призмы, ее объем?
- По каким формулам вычисляют площади боковой и полной поверхности пирамиды, усеченной пирамиды, их объем?
Домашнее задание
Тесты. Варианты I и II (см. приложение).
I уровень - решают № 1-5.
II уровень - решают № 1-7.
Ответы:
Вариант I: а); в); б); г); в); г); а).
Вариант II: б); в); в); б); б); а); в).