Функции - Повторение курса 7-9 классов

Цель: повторить основные свойства функции и построение графиков функций.

Ход урока

I. Сообщение темы и цели урока

II. Контроль усвоения материала (самостоятельная работа.

Вариант 1

1. Решите неравенство.

2. Решите систему неравенств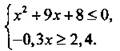

3. Решите двойное неравенство 9х2 - 2 < (3х + 2)2 < 9х2 + 2.

Вариант 2

1. Решите неравенство.

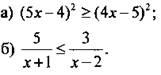
2. Решите систему неравенств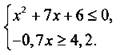

3. Решите двойное неравенство 4х2 – 3 < (2х + 3)2 < 4х2 + 3.

III. Повторение пройденного материала

Зависимость переменной у от переменной х называют функцией, если каждому значению х соответствует единственное значение у. При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.

Точка пересечения графика функции с осью ординат равна значению функции у = f(x) при х = 0, т. е. у = f(0). Точки пересечения графика функции с осью абсцисс (их еще называют нулями функции) являются корнями уравнения f(x) = 0.

Промежутки знакопостоянства функции — это те значения переменных х, при которых функция принимает положительные (у > 0) и отрицательные (у < 0) значения.

Монотонность - возрастание или убывание функции. Функция у = f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции (т. е. если х2 > х1, то и f(x2) > f(x1)). Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если х2 > х1, то f(х2) < f(x1)).

Область определения функции называется симметричной, если в нее входит и точка х0, и точка (-х0) (т. е. точка, симметричная точке х0 относительно начала координатной оси).

Функцию называют четной, если при изменении знака аргумента значение функции не меняется, т. е. f(-x) = -f(x). График четной функции симметричен относительно оси ординат.

Функцию называют нечетной, если при изменении знака аргумента значение функции также меняется на противоположное, т. е. f(-x) = -f(x). График нечетной функции симметричен относительно начала координат.

Основные виды рациональных функций

1. Линейная функция у = ах + b (где а и b - некоторые числа). График функции - прямая линия. Частные случаи:

а) у = ах - прямая пропорциональность, график проходит через начало координат;

б) у = b — прямая, параллельная оси абсцисс;

в) х = с - прямая, параллельная оси ординат.

2. Квадратичная функция у = ах2 + bх + с (где а, b, с - некоторые числа). График функции - парабола. Частный случай у = ах2. График этой функции - парабола с вершиной в начале координат.

3. Дробно-линейная функция (где b, с, d – некоторые числа). График функции - гипербола. Частный случай у = k/x - обратная пропорциональность. График этой функции - гипербола, симметричная относительно начала координат.

IV. Задание на уроке

№ 1018; 1021 (а, б, в); 1023 (а); 1025; 1028 (а, в, д); 1029 (а, г); 1030 (б); 1032 (а, в); 1033; 1034 (в); 1035 (а, в).

V. Задание на дом

№ 1019; 1021 (г, д, е); 1023 (б); 1026; 1028 (б, г, е); 1029 (б, в); 1030 (а); 1032 (б, г); 1034 (а); 1035 (б, г).

VI. Подведение итогов урока