Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Функция у = √х и ее график - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ
Цель: рассмотреть функцию у = √x , ее свойства и график.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные понятия)
Пример 1
Пусть длина стороны квадрата равна а (см), а его площадь S (см2). Величины S и а связаны соотношением S = а2, где а = 0. Это равенство означает, что каждому значению стороны квадрата а соответствует единственное значение его площади S. Из равенства S = a2 найдем а = √S. Такое соотношение означает, что для каждого значения площади квадрата S можно указать единственное значение его стороны а. Формулами S = а2 (где а ≥ 0) и a = √S задаются функциональные зависимости между одними и теми же переменными а и S. Однако в первом случае независимой переменной (аргументом) является сторона квадрата а, зависимой переменной (значением функции) — его площадь S. Во втором случае, наоборот, независимой переменной (аргументом) является площадь квадрата S, зависимой переменной (значением функции) — его сторона а. Заметим, что функция S = а2 (где а ≥ 0) и a = √S являются взаимообратными.
Пример 2
Если в предыдущем примере в каждом случае обозначить, как принято, независимую переменную буквой х, а зависимую переменную — буквой у, то получим взаимообратные функции у = х2 (где х ≥ 0) и у = √х. Сравним свойства и графики этих функций.
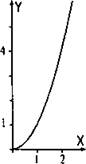
Сначала составим таблицу значений функции у = √х и построим ее график.
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
y |
0 |
1 |
1,4 |
1,7 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
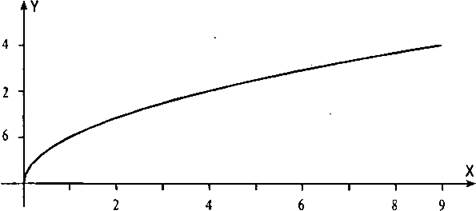
Приведем основные свойства функции у = √x:
1. Область определения функции — значения x ≥ 0.
2. Область изменения (значений) функции — значения у ≥ 0.
3. График функции пересекает оси координат в начале системы координат.
4. Значения функции у ≥ 0 при х ≥ 0 и график расположен в первой координатной четверти.
5. Функция монотонно возрастает.
Дадим определение монотонной функции. Пусть числа x1 и х2 принадлежат области определения функции и значения функции в этих точках у1 и у2 соответственно. Пусть (для определенности) х2 > х1. Если при этом для всех таких значений х1 и x2:
1) y2 > y1 (т. е. большему значению аргумента соответствует большее значение функции), то функция возрастает (график идет вверх);
2) у2 < у1 (т. е. большему значению аргумента соответствует меньшее значение функции), то функция убывает (график идет вниз).
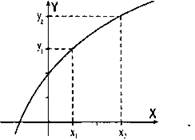
Функция возрастает (у2 > у1)
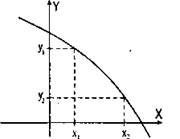
Функция убывает (у2 < у1)
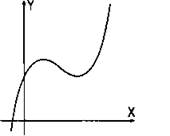
Немонотонная функция
Функция у = x2, ее свойства и график были изучены в 7 классе. Из вышесказанного рассматриваются только x ≥ 0. В этой области значений х, напомним основные свойства этой функции:
1. Область определения функции — значения х ≥ 0.
2. Область изменения (значений) функции — значения у ≥ 0.
3. График функции пересекает оси координат в начале системы координат.
4. Значения функции у ≥ 0 при х ≥ 0 и график расположен в первой координатной четверти.
5. Функция монотонно возрастает.
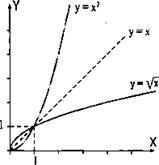
Заметим, что графики функций у = √х и у = х2 (где х ≥ 0) симметричны относительно прямой у = х (биссектрисы первого и третьего координатных углов). Доказательства этого факта, а также свойства взаимообратных функций мы в 8 классе проходить не будем.
Пример 3
Для линейной функции у = 3х - 2 найти обратную. Построить графики этих функций и убедиться, что они симметричны относительной прямой у = х.
Переменные у их связаны соотношением у = 3х - 2, что позволяет для любого значения х вычислить соответствующее значение у. Теперь из того же соотношения у = 3х - 2 выразим х: 3х = у + 2 и х = 1/3y + 2/3. Теперь можно по любому значению у найти соответствующее ему значение у, т. е. х является функцией у. Так как принято независимую переменную обозначать буквой х, а зависимую — буквой у, то в выражении х = 1/3y + 2/3 поменяем х на у, а у на х. Получаем функцию y = 1/3x + 2/3. Эта функция является обратной для данной функции у = 3х - 2.
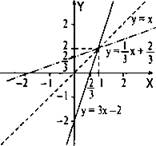
Видно, что эти графики симметричны относительной прямой у = х. На основании рисунка приведем еще некоторые свойства взаимообратных функций:
1. Монотонность таких функций одинакова. Из рисунка видно, что обе функции возрастают.
2. Если график данной функции пересекает ось абсцисс в точке х = а и ось ординат — в точке у = b, то график обратной функции, наоборот, пересекает ось абсцисс в точке х = b и ось ординат — в точке у = а. Из рисунка видно, что точки пересечения графика функции у = 3х - 2 с осями координат х = 2/3 и у = -2. Точки пересечения графика обратной функции y = 1/3x + 2/3 с осями координат, наоборот, х = -2 и у = 2/3.
III. Контрольные вопросы
1. Перечислите основные свойства функции y = √x и нарисуйте ее график.
2. Перечислите основные свойства функции у = х2 (где х ≥ 0) и нарисуйте ее график.
3. Приведите основные свойства взаимообратных функций. Что можно сказать про графики таких функций?
IV. Задание на уроке
№ 341; 342; 344; 345; 346; 349 (б, в, г); 350 (а, б, д); 351 (а, б).
V. Задание на дом
№ 340; 343; 347; 348; 349 (а, д); 350 (в, г); 351 (в, г).
VI. Творческие задания
1. Для данной функции найдите обратную. Постройте графики этих функций:
![]()
Ответы: ![]()
2. При каких значениях а и b функция у = ax + b совпадает с обратной функцией?
Ответ: а = 1, b = 0 и а = -1,6 — любое число.
Решение: Для функции у = ax + b выразим переменную х через у. Получаем: у - b = ах и ![]() (если а ≠ 0) или
(если а ≠ 0) или ![]() Обозначим независимую переменную буквой х, зависимую — буквой у. Имеем функцию
Обозначим независимую переменную буквой х, зависимую — буквой у. Имеем функцию ![]() Эта функция обратная для данной функции у = ах + b. Если эти функции совпадают, то при всех х выполняется равенство
Эта функция обратная для данной функции у = ах + b. Если эти функции совпадают, то при всех х выполняется равенство ![]() Это возможно при выполнении двух условий
Это возможно при выполнении двух условий 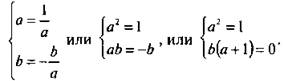
Решения первого уравнения а = ±1. Если а = 1, то при подстановке этого значения во второе уравнение получаем b · 2 = 0, откуда b = 0. В этом случае данная и обратная функции имеют вид у = х. График такой функции совпадает с осью симметрии у = х. Если а = -1, то при подстановке этого значения во второе уравнение получаем b · 0 = 0, откуда b — любое число. В этом случае данная и обратная функции имеют вид у = -х + b. График такой функции перпендикулярен оси симметрии у = х.
VII. Подведение итогов урока