Поурочное планирование по алгебре 7 класс
Функции у = х2 и у = х3 и их графики - урок 2 - ІІ четверть - Степень с натуральным показателем
ЦЕЛЬ УРОКА: Познакомить учащихся с графиком и свойствами функции у = х3. Научить строить график функции у = x3 и работать с ним.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
3 |
Устная работа |
Актуализировать опорные знания |
5 |
4 |
Изучение нового материала |
Познакомить учащихся с графиком и свойствами функции у = х3 |
6 |
5 |
Тренировочные упражнения |
Формировать умения строить график функции у = x3 и работать с ним |
24 |
6 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
2 |
7 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
ХОД УРОКА
I. Организационный момент.
II. Проверка домашнего задания (фронтально),
III. Устная работа.
1) Определить, какие точки принадлежат параболе и почему?
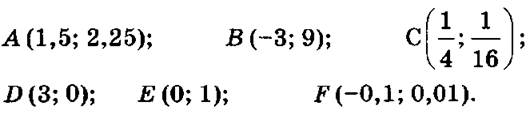
2) Вычислить:
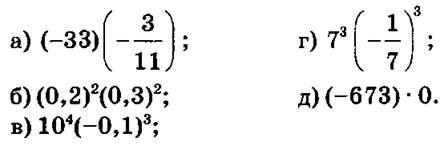
IV. Изучение нового материала (п. 23 (2 часть)).
Работа с учебником под руководством учителя. Строим на миллиметровой бумаге, используя таблицу на с. 107 п. 23 график функции у = х3 (рис. 62, 63).
Выясняем свойства функции у = х3 (с. 107). Возвращаясь к таблице на с. 107 фиксируем, что противоположным значениям х соответствуют противоположные значения у. Можно сказать название графика — кубическая парабола.
V. Тренировочные упражнения.
1) у = х3 строим график функции в тетрадях, заполняя таблицу:
x |
-2 |
-1 |
-1/2 |
0 |
1/2 |
1 |
2 |
y |
2) № 488 (с комментированием) с использованием свойства 3, желательно использовать кодоскоп;
№№ 493, 495 - комментировано;
№ 496 (на доске и в тетрадях);
№ 494 (а) (самостоятельно).
VI. Итог урока.
VII. Домашнее задание.
п. 23, №№ 489, 490, 491; 494 (б)
На уроках 45 и 46 продолжается работа с функциями. Функции, их графики составляют стержень школьного курса математики. Еще раз напоминаем понятие координатной оси, правило нахождения точки по заданной координате и правило отыскания координаты заданной точки.
Напоминаем все термины, связанные с декартовыми координатами на плоскости (абсцисса, ордината, ось абсцисс, ось ординат, координатные четверти).
Повторяем с учащимися правило отыскания точки по заданным координатам и правило отыскания координат точек на плоскости.