Поурочное планирование по алгебре 7 класс
Прямая пропорциональность и ее график - ІI четверть - Функции
ЦЕЛЬ УРОКА: Формирование понятия прямой пропорциональности и ее графика.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
|
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
|
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
|
3 |
Фронтальная работа с классом |
Актуализация опорных знаний |
7 |
|
4 |
Изучение нового материала |
Ввести понятие прямой пропорциональности и ее графика |
8 |
|
5 |
Тренировочные упражнения |
Формировать понятие прямой пропорциональности, умение строить ее график и работать с ним |
20 |
|
6 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
2 |
|
7 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
|
ХОД УРОКА
I. Организационный момент.
II. Проверка домашнего задания (по кодоскопу).
III. Фронтальная работа с классом.
Устно:
1) В одном ящике 5 кг чая, в другом 8 кг. Весь чай распределяют по пачкам по х г. в каждой пачке. Обозначив количество получившихся пачек буквой у, выразить зависимость у от х формулой 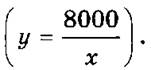
Найти:
а) значение у, если х = 100;
б) значение х, если у = 100.
2) 15% от числа х равны у.
Задать формулой функцию у от х. Какова область определения этой функции?
IV. Изучение нового материала (работа с учебником, п. 15).
1) Привести пример зависимости двух величин, которую можно задать формулой у = kx, k ≠ 0.
2) Как называют функцию у = kx, k ≠ 0?
3) Что представляет собой график прямой пропорциональности?
4) На рис. 26 изображены 4 графика прямой пропорциональности. Какой знак имеет коэффициент k для каждого из графиков?
V. Тренировочные упражнения.
№ 298 — устно;
№№ 297, 306 — самостоятельно с последующей проверкой;
№ 299 — самостоятельно с последующей проверкой. Возможно оформление в виде таблицы:
x |
-9 |
0 |
1 |
4 |
||||
y |
0 |
-1/2 |
10 |
1 |
№ 300 — на доске и в тетрадях; №№ 308, 303 — устно.
VI. Итог урока.
Какая функция называется прямой пропорциональностью? Что представляет собой ее график?
VII. Домашнее задание.
п. 15; №№ 301, 309, 310, 312 (а, б).
В упражнениях п. 15 ученики должны:
1. Понять, что в прямой пропорциональной зависимости величин у = kx отношение величин y/x не меняется (в данной задаче);
2. Уметь строить график зависимости у = kx по 2 точкам (одна из которых — начало координат, а другую лучше выбирать так, чтобы между ними был промежуток больше, тогда график будет точнее и погрешность чертежа меньше);
3. По графику уметь находить для данного значения х соответствующее значение у и наоборот. Желательно вместе с учениками выработать алгоритм, он пригодится в дальнейшем;
4. Знать расположение графика при k > 0, k < 0;
5. Полезно научить видеть на чертеже положительные и отрицательные ординаты.
Например:
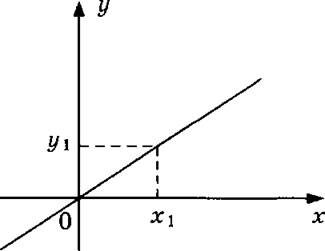
1. Показать точки оси х для которых х > 0.
2. Показать точки оси х для которых д: < 0.
3. На оси х взята точка х1. Показать соответствующую ей ординату.
4. Что можно сказать о знаке у1?
5. Что можно сказать о всех ординатах этого графика при х > 0?
Аналогичную работу можно проводить и при изучении линейной функции.
Желательно также предложить ряд упражнений на отыскание функциональной зависимости между переменными величинами в аналитической форме, если дана их табличная зависимость:
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
y |
3 |
4 |
5 |
6 |
7 |
? |
? |
1. Сравнить соответствующие значения у и х (у больше х на 2)
2. Что надо написать в пропущенных местах?
3. Что надо сделать с х, чтобы получить у! (к х прибавить 2).
4. Написать формулу, связывающую у и х(у = х + 2).
5. Как называется такая зависимость?
Аналогично можно поработать с таблицей
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
y |
0 |
2 |
4 |
6 |
8 |
? |
? |