Решение задач с помощью уравнений - урок 2 - I четверть - Выражения, тождества, уравнения

ЦЕЛЬ УРОКА: Выработка навыка решения задач с помощью уравнений.

ПЛАН УРОКА:

№	Этап урока	Содержание	Время (мин)
1	Организационный момент	Нацелить учащихся на урок	1
2	Проверка домашнего задания	Коррекция ошибок	5
3	Устная работа	Актуализировать опорные знания	5
4	Тренировочные упражнения	Формировать умение решать текстовые задачи с помощью уравнений	21
5	Самостоятельная работа	Коррекция ошибок	10
6	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке	1
7	Сообщение домашнего задания	Разъяснить содержание домашнего задания	2

ХОД УРОКА

I. Организационный момент

II. Проверка домашнего задания:

№№ 153, 165

III. Устная работа.

1) № 166.

2) Мой ежедневный расход составляет 5х руб. У меня т рублей. Сколько денег у меня останется по истечении недели? (m – 35x)

3) Колесо поворачивается на а метров за один час.

Сколько метров оно сделает за х минут?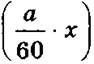

4) а рабочих выполняют работу за t дней. За сколько дней выполнят ту же работу х рабочих (при тех же условиях работы)?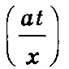

5) Поезд шел х часов со скоростью v км/ч, а затем еще z часов со скоростью v1 км/ч. Какова средняя скорость поезда за это время?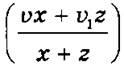

IV. Тренировочные упражнения.

№№ 159, 161, 162 — на доске.

V. Самостоятельная работа (с последующей проверкой по кодоскопу).

Вариант I

1) В двух ящиках 48 кг слив. В одном из них на 8 кг больше, чем в другом. Сколько килограммов слив в каждом ящике?

2) Решить уравнение:

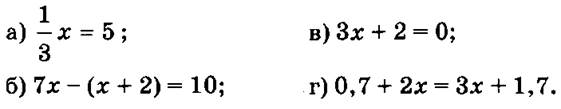
3) № 137 (а).

Вариант II

1) Веревку длиной 96 м разрезали на две части так, что одна из них оказалась в 3 раза длиннее другой. Найти длину каждой части.

2) Решить уравнение:

3) № 137 (б).

VI. Итог урока.

VII. Домашнее задание.

п. 8, №№ 149, 150, 158, 160, 241, (а, в).

На уроках №15 -№19 систематизируются сведения о решении уравнений с одним неизвестным.

Усиливается роль теоретических сведений при рассмотрении уравнений. Вводится понятие корня уравнения. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится понятие равносильности уравнений, формируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней.

Особое внимание уделяется решению уравнений вида ах = b при различных значениях а и b. Продолжается работа по формированию у учащихся умений использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в VI классе.

Умение решать полученные из условия задачи уравнения является необходимым условием решения задачи, но не достаточным. Чтобы учащиеся смогли воспользоваться уравнениями при решении текстовых задач, нужно научить их выражать в математической (аналитической) форме зависимость между числами (величинами).

Работа по изучению способов выражения зависимости может проводиться в такой последовательности.

Разъясняем учащимся, что при выполнении арифметических действий мы пользуемся знаками действий и знаком равенства, например: 6 + 9 = 15.

Это равенство означает, что сумма чисел 6 и 9 равна 15, или, что одно и то же, что в результате прибавления к 6 числа 9 получается 15.

Следовательно, равенство 6 + 9 = 15 устанавливает связь (зависимость) между числами 6, 9 и 15. Однако связь между этими же числами, устанавливаемую равенством 6 + 9 = 15, можно сформулировать иначе.

Например: 15 больше 6 на 9;

15 больше 9 на 6;

6 меньше 15 на 9;

9 меньше 15 на 6;

6 в сумме с 9 дает 15.

Таким образом любое из приведенных предложений, устанавливающее связь между числами 6, 9 и 15 или зависимость между ними, может быть выражено равенство.

6 + 9 = 15.

Рассмотрим обратную задачу:

Выразить равенством зависимость между числами, установленную предложением: 15 больше 6 на 9. Эту зависимость можно выразить так:

6 + 9 = 15; 15 - 6 = 9; 15 - 9 = 6.

Для практических целей достаточно уметь выражать словесно сформулированную связь между величинами в виде хотя бы одного равенства.

Из истории математики.

Египтяне имели особый знак для обозначения неизвестного числа, который переводили словом «куча» («куча» или неизвестное количество единиц).

Вот одна из задач папируса Ахмеса (его относят к эпохе около 1700 лет до начала нашего летоисчисления, написан в Египте): «Куча и ее седьмая часть 19. Найти кучу». Запись задачи нашими знаками приводит к уравнению х + 1/7 х = 19.

Способ решения этой задачи, примененный древним автором Ахмесом, называемый методом одного ложного положения, мы не приводим.

У разных народов применялся метод двух ложных положений. Вот его объяснение, данное неким арабским автором:

«Надо решить уравнение х + 2/3x + 1 = 10.

Вот как поступай.

Черти весы и на точке опоры напиши 10. Положи на левую чашу весов какое угодно число, например, 9, и сосчитай, сколько получится в левой половине равенства при х равном девяти: 9 + 6 + 1 = 16. Это больше, чем требуется, на 16 - 10 = 6.

Запиши число 9, которое есть первое положение, на левой чаше весов, а число 6, которое есть первое отклонение, над левой чашей.

Теперь положи на правую чашу другое какое-нибудь число, например 6, и подсчитай, что при х = 6 получается в левой половине равенства:

6 + 4 + 1 = 11.

Запиши число 6, которое есть второе положение, на правой чаше, 11 – 10 = 1, которое есть второе отклонение, над чашею

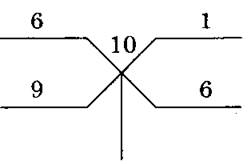
Умножай первое положение на второе отклонение и второе положение на первое отклонение и разность произведений дели на разность второго и первого отклонений:

Если бы вместо положений 9 и 6 взяли 9 и 3, то имели бы первое отклонение 6; второе положение 3 дало бы при подстановке 3 + 2 + 1 = 6, на 4 меньше 10. Отклонение «меньше» запишем под весами:

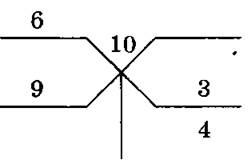
Правило: в случае, когда отклонения записаны по разные стороны от весов, нужно вычислить сумму произведений первого положения на второе отклонение и второго положения на первое отклонение и разделить на сумму отклонений.

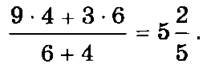
Способом двух ложных положений можно решать всякие уравнения первой степени с одним неизвестным вида ах + b = с».

Легко убедиться, что число 52/5 действительно является корнем уравнения