Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Зачет по теме Многочлены - ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ - МНОГОЧЛЕНЫ
Цели: сравнить успеваемость учащихся при одинаковой сложности заданий; иметь возможность повысить оценки за выполненные контрольные работы.
Тип уроков: уроки контроля, оценки и коррекции знаний.
Ход уроков
I. Сообщение темы и целей уроков
II. Общая характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в блоке А, более сложные — в блоке В, еще сложнее — в блоке С. Каждая задача из блока А оценивается 1 баллом, из блока В — 2 баллами, из блока С — 3 баллами. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка “3” ставится за 6 баллов, оценка “4” — за 10 баллов, оценка “5” — за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Работа рассчитана на два урока.
III. Зачетная работа
Вариант 1
А
1. Выполните действия:
2. Упростите выражение 
и вычислите его значение при х = 11/24.
3. Приведите выражение 
к многочлену стандартного вида и определите его степень.
4. Решите уравнение:
5. Разложите на множители многочлен:
6. Докажите, что выражение 214 - 75 + 144 кратно 90.
7. Поезд проехал третью часть расстояния между городами со скоростью 40 км/ч, а оставшийся путь — со скоростью 60 км/ч. Поездка заняла 7 ч. Найдите расстояние между городами и среднюю скорость поезда.
В
8. Найдите значение выражения 
9. Разложите на множители выражение:
10. Решите графически уравнение 2х - 3 = х - 1.
11. Петя задумал число и прибавил к нему 5. Результат умножил на 7. Потом вычел удвоенное задуманное число. Полученное число разделил на 5. Потом вычел задуманное число. Какое число получил Петя?
С
12. Упростите выражение 
13. Решите уравнение 
14. При каком значении параметра а уравнения 
имеют общий корень?
Вариант 2
А
1. Выполните действия:
2. Упростите выражение 
и вычислите его значение при х = 2/5.
3. Приведите выражение 
к многочлену стандартного вида и определите его степень.
4. Решите уравнение:
5. Разложите на множители многочлен:
6. Докажите, что выражение 274 - 95+ 184 кратно 88.
7. Поезд проехал четвертую часть расстояния между городами со скоростью 50 км/ч, а оставшийся путь — со скоростью 30 км/ч. Поездка заняла 6 ч. Найдите расстояние между городами и среднюю скорость поезда.
В
8. Найдите значение выражения 
9. Разложите на множители выражение:
10. Решите графически уравнение 4 - 2х = х + 1.
11. Вася задумал число и прибавил к нему 7. Результат умножил на 5. Потом прибавил удвоенное задуманное число. Полученное число разделил на 7. Потом вычел задуманное число. Какое число получил Вася?
С
12. Упростите выражение 
13. Решите уравнение (х2 + 5х)2 + 6(х2 + 5х) = 0.
14. При каком значении параметра а уравнения 5(х - 4) = 3(х - 2) и 3х2 + 2ах - 5 = 0 имеют общий корень?
IV. Разбор задач (ответы и решения)
Вариант 1
А
1. 
2. 24x + 9; 20.
3. -2а3b2 + 6ab2, пятая степень.
4. 
б) х — любое число, кроме нуля.
5. а) 3ху(х + 2 - 5ху); б) (у + 2)(х + 7).
6. Доказано.
7. 360 км; 
км/ч.
В
8. 60.
9. 
10. x = 2.
11. 7.
С
12. В данном выражении выполним все указанные действия:
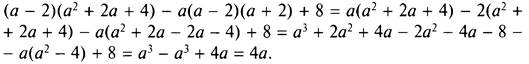
(Ответ: 4а.)
13. В левой части уравнения (х2 - 3х)2 + 2(х2 - 3х) = 0 вынесем общий множитель х2 + 3х за скобки. Получаем (х2 - 3х)(х2 - 3х + 2) = 0. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, т. е. х2 - 3х = 0 или х2 - 3х + 2 = 0. Решим эти уравнения разложением на множители.
а) Вынесем общий множитель х за скобки: х(х - 3) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем х = 0 или х - 3 = 0 (корень этого уравнения х = 3).
б) Представим член -3х в виде -3х = -х - 2х и используем группировку членов. Получаем х2 – х - 2х + 2 = 0, или (х2 - х) + (-2х + 2) = 0, или х(х - 1) - 2(х - 1) = 0, или (х - 1)(х - 2) = 0.
Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: х - 1 = 0 (корень х = 1) и х - 2 = 0 (корень х = 2).
Итак, данное уравнение имеет четыре корня.
(Ответ: х = 0, х = 3, х = 1, х = 2.)
14. Сначала решим линейное уравнение 6(х - 3) = 2(х + 1). Раскроем скобки и получим 6х - 18 = 2х + 2, или 6х - 2х = 18 + 2, или 4х = 20, откуда х = 5.
По условию это число является и корнем второго уравнения 2х2 + 3ах – 1 = 0. Подставим корень в это уравнение и получим 2 ∙ 52 + 3а ∙ 5 - 1 = 0, или 50 + 15а - 1 = 0, или 15а = -49, откуда 
При таком значении а два данных уравнения имеют общий корень х = 5.
(Ответ: 
)
Вариант 2
А
1. 
2. -15х - 4; -10.
3. -3а3b2 + 5ab2, пятая степень.
4. 
б) х - любое число, кроме нуля.
5. а) 4ху(у - 2 + 3 ху); б) (х + 5)(y + 3).
6. Доказано.
7. 200 км; 
км/ч.
В
8. 18.
9. 
10. х = 1.
11. 5.
С
12. В данном выражении выполним все указанные действия:
(Ответ: а.)
13. В левой части уравнения (х2 + 5х)2 + 6(х2 + 5х) = 0 вынесем общий множитель х2 + 5х за скобки. Получаем (х2 + 5х)(х2 + 5х + 6) = 0. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, т. е. х2 + 5х = 0 или х2 + 5х + 6 = 0. Решим эти уравнения разложением на множители.
а) Вынесем общий множитель х за скобки: х(х + 5) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем х = 0 или х + 5 = 0 (корень этого уравнения х = -5).
б) Представим член 5х в виде 5х = 2х + 3х и используем группировку членов. Получаем х2 + 2х + 3х + 6 = 0, или (х2 + 2х) + (3х + 6) = 0, или х(х + 2) + 3(х + 2) = 0, или (х + 2)(х + 3) = 0.
Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: х + 2 = 0 (корень х = -2) и х + 3 = 0 (корень х = -3).
Итак, данное уравнение имеет четыре корня.
(Ответ: х = 0, х = -5, х = -2, х = -3.)
14. Сначала решим линейное уравнение 5(х - 4) = 3(х - 2). Раскроем скобки и получим 5х - 20 = 3х - 6, или 5х - 3х = 20 - 6, или 2х = 14, откуда х = 7.
По условию это число является и корнем второго уравнения 3х2 + 2ах - 5 = 0. Подставим корень в это уравнение и получим 3 ∙ 72 + 2а ∙ 7 - 5 = 0, или 147 + 14а - 5 = 0, или 14а = -142, откуда 
При таком значении а два данных уравнения имеют общий корень х = 7.
Ответ: 
V. Подведение итогов уроков