Полный справочник школьника 1-4 класссы - 2015 год
Различные случаи письменного деления - УМНОЖЕНИЕ И ДЕЛЕНИЕ - МАТЕМАТИКА
Пример 1
459 : 3
1) Определяем первое неполное делимое. Это 4 сотни.
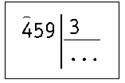
2) Определяем количество цифр в частном. Их будет три: сотни, десятки, единицы.
3) Делим первое неполное делимое 4 на 3. Ближайшее меньшее число 3 (оно делится на 3 без остатка): 3 : 3 = 1. Цифра 1 — первая цифра в частном. Из 4 вычитаем 3, находим остаток 1. Проверяем: остаток меньше делимого, 1 < 3.
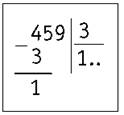
4) Сносим следующую цифру — 5. Второе неполное делимое (15) делим на 3. Оно делится без остатка: 15 : 3 = 5. Пишем цифру 5 в частном. Находим остаток: 15 - 15 = 0, нуль не пишем.

5) Сносим последнюю цифру — 9. Делим 9 на 3. Получилось 3. Записываем цифру 3 в частном и находим остаток: 9 - 9 = 0. Остатка нет. Число поделилось полностью.
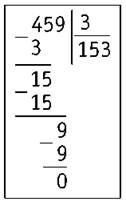
6) Читаем ответ: частное равно 153.
В некоторых случаях первое неполное делимое — двузначное число.
Пример 2
258 : 3
1) Определяем первое неполное делимое.
2 на 3 разделить нельзя, поэтому берём две цифры делимого — 25. Это и есть первое неполное делимое, с которого мы начнём решение примера.
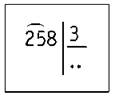
2) Определяем количество цифр в частном. Их будет две: десятки и единицы.
3) Делим первое неполное делимое 25 на 3. Ближайшее наименьшее число, которое делится на 3 без остатка, — 24. 24 : 3 = 8. Записываем в частном первую цифру — 8. 8 · 3 = 24. Записываем под первым неполным делимым 24. Из 25 вычитаем 24, находим остаток 1.
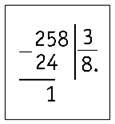
4) Проверяем: остаток меньше делителя, 1 < 3. Записываем единицу под четвёркой.
5) Сносим 8. Второе неполное делимое — 18. Делим 18 на 3. Получилось б. Записываем цифру б в частном и находим остаток: 18 - 18 = 0, остатка нет. Число поделилось полностью.
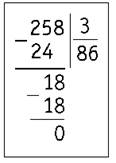
6) Читаем ответ: частное равно 86.
Деление круглых чисел выполняется по тем же правилам.
Пример 3
22720 : 4
1) Определяем первое неполное делимое — 22.
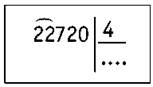
2) Определяем количество цифр в частном. Их будет четыре: тысячи, сотни, десятки, единицы.
3) Ближайшее наименьшее к 22 число, которое делится на 4 без остатка, — 20. 20 : 4 = 5. Записываем в частном первую цифру 5.
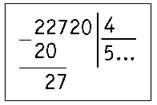
4) Далее выполняем деление следующего делимого и далее по порядку.
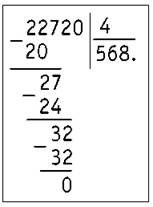
5) Последняя цифра (0) просто переносится из делимого в частное.

Деление многозначного числа на круглое
1. Деление на круглое число с остатком.
Пример
440 : 60
1) Первое неполное делимое — 440. В частном будет одна цифра.
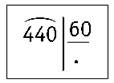
2) Делим и делимое, и делитель на 10. Получаем: 44 : 6. Берём по 7.
3) Определяем, какое число разделим. Для этого умножаем 7 на 60. Получается 420.
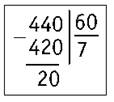
4) Находим остаток: 440 - 420 = 20.
5) Проверка: 60 · 7 + 20 = 420 + 20 = 440.
6) Читаем ответ: частное 7, остаток 20.
2. Деление многозначного числа на круглое без остатка.
Пример
12 750 : 30
1) Определяем первое неполное делимое — 127.
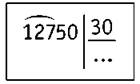
2) Определяем количество цифр в частном. Их будет три.
3) Числа 127 и 30 делим на 10. 12 : 3 = 4. Записываем 4 в частном. Умножаем 4 на 30. Получилось 120. Находим остаток: 127 - 120 = 7. Остаток 7 < 30.
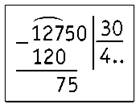
4) Сносим следующую цифру (5) и записываем рядом с остатком. Второе неполное делимое — 75.
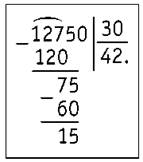
5) Делим 75 и 30 на 10, а затем 7 : 3. Получилось 2. Записываем 2 в частном. Умножаем 2 на 30. Получилось 60. Находим остаток: 75 - 60 = 15. Остаток 15 < 30.
6) Сносим последнюю цифру (0) и записываем рядом с остатком. Третье неполное делимое — 150. 150 и 30 делим на 10, а затем 15 : 3. Получилось 5.
Записываем 5 в частном. 30 · 5 = 150. Остатка нет.

7) Читаем ответ: частное равно 425.
Случаи деления на однозначное число, когда 0 в частном
Пример
24 320 : 4
1) Определяем первое неполное делимое.
2) Определяем количество цифр в частном. Их будет четыре: тысячи, сотни, десятки, единицы.
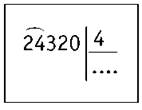
3) Делим 24 на 4. Получилось б. Находим остаток: 24 - 24 = 0. Остатка нет.
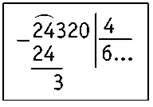
4) Сносим следующую цифру — 3. Число 3 на 4 не делится. Записываем в частном 0.
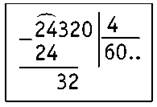
5) Сносим следующую цифру (2) и записываем её после цифры 3. Получилось число 32. Делим 32 на 4. Получилось 8. Находим остаток: 32 - 32 = 0. Остатка нет.
6) Последняя цифра делимого — 0, переносим её в частное.
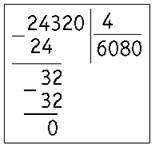
7) Читаем ответ: частное равно б 080.
Деление многозначного числа на двузначное
Деление без остатка трёхзначного числа на двузначное, если в частном получается однозначное число.
Пример
315 : 63
1) Чтобы найти цифру в частном, заменяем делитель ближайшим круглым числом. Это число 60.
2) Делим 315 на 60. Для этого достаточно разделить 31 на 6. Пробная цифра 5.
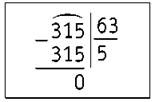
3) Умножаем 63 на 5 (устно). Получаем 315. Значит, цифра 5 подходит.
4) Читаем ответ: частное равно 5.
Если при делении на двузначное число в частном получается одна цифра (однозначное число), то её можно найти методом подбора. Для этого нужно посмотреть на последнюю цифру в делителе и делимом и, пользуясь таблицей умножения, подобрать цифру в частном.
Деление без остатка многозначного числа на двузначное, если в частном получается многозначное число.
Пример
27 904 : 64
1) Определяем первое неполное делимое — 279.

2) Определяем количество цифр в частном. Их будет три: сотни, десятки, единицы.
3) Чтобы найти первую цифру в частном, нужно делимое 279 и делитель 64 разделить на 10, то есть закрыть по одной цифре справа. Делим 27 на 6. Ближайшее число, которое делится на 6, — 24.
Делим 24 на 6. Получилось 4. Это пробное число.
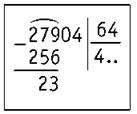
4) Проверяем пробное число 4: 64 · 4 = 256.
5) Вычитаем число 256 из 279. Остаток — 23, 23 < 64. Значит, цифра 4 подобрана верно.
6) Сносим следующую цифру (0) и записываем её рядом с остатком. Получилось число 230. Это второе неполное делимое.
7) Делим 230 на 64. Закрываем в делимом и делителе по одной цифре справа: 23 : 6. Берём по 3. Проверяем цифру 3. Умножаем 64 на 3. Получилось 192. Находим остаток: 230 - 192. Получилось 38.

8) Сравниваем остаток и делитель. Остаток меньше. Значит, цифра 3 подобрана верно.
9) Сносим следующую цифру (4) и записываем рядом с остатком 38. Это число 384. Третье неполное делимое — 384.
10) Определяем последнюю цифру в частном по последней цифре делителя. В таблице умножения на 4 находим число, которое при умножении на 4 оканчивается цифрой 4. Это число 6. Проверяем: 64 · 6 = 384. Находим остаток: 384 - 384 = 0. Деление закончено.

11) Читаем ответ: частное равно 436.
Деление многозначного числа на трёхзначное
При делении на трёхзначное число используются те же приёмы, что и при делении на двузначное число.
Пример
37 294 : 643
1) Определяем первое неполное делимое — 3 729.
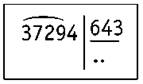
2) Определяем количество цифр в частном. Их будет две: десятки и единицы.
3) Чтобы 3 729 разделить на 643, достаточно 37 разделить на 6. Берём по 6.
4) Проверяем цифру 6: 64 · 6 = 384. Это число больше, чем 372. Цифра 6 не подходит.
5) Проверяем цифру 5: 64 · 5 = 320, 320 < 372. Цифра 5 подходит. Записываем её в частном. Определяем, сколько десятков разделили: 643 · 5 = 3 215.
6) Находим остаток: 3 729 - 3 215 = 514. Остаток 514 < 643, значит, цифра подобрана верно.
7) Сносим цифру 4. Второе неполное делимое — 5 144. Чтобы 5 144 разделить на 643, достаточно 51 разделить на 6. Пробная цифра 8.
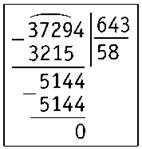
8) Проверяем цифру 8: 643 · 8 = 5 144. Цифра 8 подходит.

Читаем ответ: частное равно 58.