Урок решения задач по теме «Равномерное движение» - ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Цель: научить решать задачи по теме «Равномерное движение».

Ход урока

I. Повторение. Беседа

1. Что такое вектор перемещения? Что он характеризует?

2. Как записывается в векторной форме уравнение равномерного прямолинейного движения?

3. Как записывается в координатной форме уравнение равномерного прямолинейного движения точки если она движется по оси оу, по оси ох?

4. Какое движение называется равномерным прямолинейным?

5. Почему при равномерном прямолинейном движении за любые равные промежутки времени тело перемещается на одно и то же расстояние?

II. Решение задач

1. Какова траектория движения точек винта вертолета по отношению к летчику? по отношению к Земле?

Решение: По отношению к летчику траектория точек винта вертолета - окружность; по отношению к Земле - винтовая линия, так как вертолет совершает поступательное движение.

2. Скоростной лифт в высотном здании поднимается равномерно со скоростью 3 м/с. Начертить график перемещения. Определить по графику время, в течение которого лифт достигнет высоты 90 м (26-й этаж).

Дано:

V = 3 м/с

у = 90 м

у₀ = 0.

Найти:

t - ?

Решение:

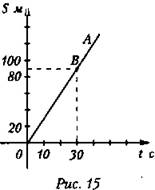
Пусть ось у совпадает с направлением движения лифта, а начало оси - с точкой, в которой лифт находится в начальный момент времени. S = у – у₀; у = 0t. Следовательно, S = 0t (т. к. у₀= 0). Для построения графика перемещения отложим по оси абсцисс время Т. а по оси ординат - перемещение S.

Зависимость перемещения от времени изобразится прямой ОА. Для построения прямой линии достаточно двух точек. Выбираем произвольно момент времени и определяем для него перемещение. Результат записываем в таблицу:

Т	0	20
S	0	60

S = 3t - уравнение перемещения.

Отмечаем точки на координатной плоскости и строим прямую ОА. Тангенс угла наклона прямой ОА к оси t численно равен скорости V.

По графику определяем время, в течение которого лифт достигнет высоты 90 м. Для этого восстановим перпендикуляр из точки S = 90 м до пересечения с прямой ОА; из точки В пересечения перпендикуляра и прямой опустим другой перпендикуляр к оси t.

По графику видно, что лифт достигнет высоты 90 м через 30 с. (Ответ: t = 30 с.)

3. Из двух точек А и В, расположенных на расстоянии 90 м друг от друга, одновременно в одном направлении начали движение два тела. Тело, движущееся из точки А, имело скорость 5 м/с, а тело движущееся из точки В, - скорость 2 м/с. Через какое время первое тело нагонит второе? Какое перемещение совершит каждое тело?

Задачу можно решить двумя способами: аналитическим и графическим.

Решение:

1 способ (аналитический)

Дано.

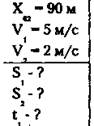
Решение:

Выберем начало оси X в точке А и направим ее по движению тел. Тогда уравнения движения тел таковы:

Х₁ = V₁t, X₀₁ = 0, - начальная координата первого тела.

X₂ = X₀₂ + V₂t. X₁ и X₂ - координаты первого и второго тела.

Для точки С, в которой первое тело нагонит второе, X₁ = X₂, t = t₁. Тогда с учетом X₁ и X₂ получим: V₁t₁ = X₀₂ + V₂t₁, гдё t₁ - время движения тел до точки встречи С. Из этого уравнения находим время движения тел:

Найдем перемещение тел:

2 способ (графический)

Отложим в масштабе по оси абсцисс время t движения, а по оси ординат - значение координаты X. Запишем уравнения движения тел с учетом условия задачи:

Изобразим графически зависимость координат от времени прямыми 1 и 2.

Для каждой прямой можно составить таблицу:

X1 = 5t				X2 = 90 + 2t
X1	0	50		X2	90	110
Т	0	100		T	0	10

Найдем координаты их точки пересечения С: t₁ = 30 с, X₁ = Х₂ = 150 м. Следовательно, первое тело нагонит второе через 30 с. Перемещения тел соответственно равны.

(Ответ: S₁ = 150 м; S₂ = 60 м; t₁ = 30 с.)

4. Уравнение движения тела дано в виде X = 4 - 3t. Определить начальную координату тела, скорость движения и перемещение тела за 2 секунды. (Уравнение записать в СИ). (Ответ: Х₀= 4 м; V_x = -3 м/с; S = -6 м.)

5. По заданным графикам напишите уравнения движений X = Х(t). Из уравнений и графиков найдите координаты тел через 5 с, время и место встречи тел II и III.

Решение:

Графики говорят о равномерном прямолинейном движении тел II и III, общая формула которого: X = X₀ + V_xt.

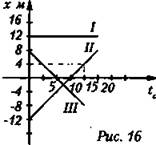
Тело I покоится, т. к. с течением времени координата не меняется. Уравнение движения: Х₁ = 2; V₁ = 0.

Тело II. Координата этого тела увеличивается с течением времени; следовательно, направление скорости движения и оси О_х совпадают. Скорость тела можно определить из уравнения движения: X = Х₀ + Vt → V = (X - X₀)/t. По графику движения нужно определить начальную координату тела и координату через некоторый промежуток времени (произвольный). Очевидно: Х₀= -12 м; зададим значение времени t = 15 с. Из этой точки на оси времени восстанавливаем перпендикуляр до пересечения с графиком движения; затем из точки пересечения опускаем перпендикуляр на ось О_х и определяем координату, соответствующую этому времени. Записываем:

Уравнение движения:

Тело III. Координата тела с течением времени уменьшается; следовательно, его скорость направлена противоположно избранному направлению оси О_х. Тело вначале (5 с) приближается к началу координат, а затем удаляется от него в противоположную сторону. Тело III движется навстречу телу II.

В момент t = 0 х₀ = 8 м. Аналогично найдем скорость движения.

Уравнение движения: Х_III = 8 - 1,6t; при t₁ = 5 с → x_III = 0.

Точка А - момент встречи тел II и III. Тела встречаются через t = 7,5 с в точке с координатой x = -4 м. Место и время встречи тел можно определить и аналитически, если учесть, что для момента встречи тел Х_II = Х_III, то есть

Подставив значение t в одно из уравнений, найдем X = -4 м.

6. По графику перемещения (а) построить график скорости и определить характер движения тела относительно оси х(V).

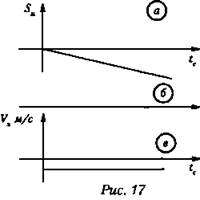
Решение:

Из графика следует, что тело движется равномерно и прямолинейно в отрицательном направлении оси х, поскольку проекция S_x вектора перемещения на ось x отрицательна и возрастает по абсолютному значению прямо пропорционально времени. Тело движется в направлении, противоположном оси О_х и проекция вектора скорости тоже будет отрицательна. Графиком скорости будет являться прямая, параллельная оси времени.

7. Теплоход на подводных крыльях шел вниз по реке со скоростью V = 80 км/ч, а вверх - со скоростью V в стоячей воде и скорость V₂ течения реки. (Ответ: V₁ = 78 км/ч (собственная скорость теплохода); V₂ = 2 км/ч (скорость течения реки).

8. Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 55 секунд. По неподвижному эскалатору пассажир мог бы подняться за 3,5 минуты. За какое время поднимается пассажир по движущемуся эскалатору? (Ответ: 44 секунды.)

9. Сколько времени пассажир, сидящий у окна поезда, идущего со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого V₂ = 36 км/ч, длина поезда 150 м? (Ответ: 6 секунд).

10. Лодка движется поперек реки перпендикулярно ее берегам со скоростью 2 м/с. Под каким углом к выбранному направлению оси у и с какой скоростью относительно поверхности воды гребец держит курс, если скорость течения реки 5 км/ч? (Ответ: V₂ ≈ 2,4 м/с; α ≈ 0,84 рад.)

11. Скорость вертикального подъема груза краном V₁ = 0,2 м/с, скорость тележки крана V₂ = 0,1 м/с. Определите скорость движения груза относительно Земли. (Ответ: 0,22 м/с).

12. Лодочник перевозит пассажиров с одного берега на другой за время t = 10 мин по траектории АВ. Скорость течения реки V_p = 03 м/с, ширина реки 240 м. С какой скоростью V относительно воды и под каким углом а к берегу должна двигаться лодка, чтобы достичь другого берега за указанное время? (Ответ: V’ = 0,5 м/с, α = 53°.)

III. Самостоятельная работа

Вариант 1

1. Автомобиль дважды проехал вокруг Москвы по кольцевой дороге, длина которой 109 км. Чему равны пройденный автомобилем путь l и модуль его перемещения S?

А. l = 109 км; S = 0 км.

Б. l = 218 км; S = 0 км.

В. l = S = 218 км.

Г. l = S = 0 км.

2. Вертолет равномерно поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с корпусом вертолета?

А. Точка.

Б. Прямая.

В. Окружность.

Г. Винтовая линия.

3. Пловец плывет по течению реки. Чему равна скорость пловца относительно берега реки, если скорость пловца относительно воды 1,5 м/с, а скорость течения реки 0,5 м/с?

А. 0,5 м/с.

Б. 1 м/с.

В. 1,5 м/с.

Г. 2 м/с.

4. Плот равномерно плывет по реке со скоростью 6 км/ч. Человек движется поперек плота со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?

А. 2 км/ч.

Б. 7 км/ч.

В. 10 км/ч.

Г. 14 км/ч.

5. По графику зависимости пройденного пути от времени (рис. 18) определите скорость велосипедиста в момент времени t = 2 c.

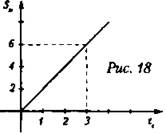
А. 2 м/с.

Б. 3 м/с.

В. 6 м/с.

Г. 18 м/с.

6. На рис. 19 представлены три графика зависимости пройденного пути от времени. Какое из тел двигалось с большей скоростью?

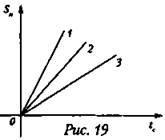
А. 1.

Б. 2.

В. 3.

Г. Скорости всех трех тел одинаковы.

7. Поезд длиной 200 м въезжает в тоннель длиной 300 м, двигаясь равномерно со скоростью 10 м/с. Через какое время поезд выйдет полностью из тоннеля?

А. 10 с.

Б. 20 с.

В. 30 с.

Г. 50 с.

8. Две моторные лодки движутся вдоль реки навстречу друг другу. Скорости лодок относительно воды равны 3 м/с и 4 м/с соответственно. Скорость течения реки равна 2 м/с. Через какое время после их встречи расстояние между лодками станет равным 84 м?

А. 12 с.

Б. 21 с.

В. 28 с.

Г. 42 с.

9. Лодка подтягивается лебедкой к берегу (рис. 20). Скорость наматывания каната на лебедку постоянна и равна . С какой скоростью движения лодка в момент, когда канат составляет угол а с вертикалью?

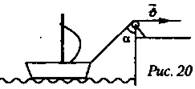
10. Половину пути автомобиль проходит с постоянной скоростью V₁, а вторую половину пути - со скоростью V₂, двигаясь в том же направлении. Чему равна средняя скорость автомобиля?

Вариант 2

1. Спортсмен пробежал дистанцию 400 м по дорожке стадиона и возвратился к месту старта. Чему равен путь l, пройденный спортсменом, и модуль его перемещения S?

А. l = S = 0 м.

Б. l = S = 400 м.

В. l = 400 м; S = 0 км.

Г. l = 0 м; S = 400 м.

2. Вертолет равномерно поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с землей?

А. Точка.

Б. Прямая.

В. Окружность.

Г. Винтовая линия.

3. Пловец плывет против течения реки. Чему равна его скорость относительно берега реки, если скорость пловца относительно воды 1,5 м/с, а скорость течения реки 0,5 м/с?

А. 0,5 м/с.

Б. 1 м/с.

В. 1,5 м/с.

Г. 2 м/с.

4. Кран равномерно поднимает груз вертикально вверх со скоростью 03 м/с и одновременно равномерно и прямолинейно движется по горизонтальным рельсам со скоростью 0,4 м/с. Чему равна скорость груза в системе отсчета, связанной с Землей?

А. 0,1 м/с.

Б. 0,35 м/с.

В. 0,5 м/с.

Г. 0,7 м/с.

5. По графику зависимости пройденного пути от времени (рис. 21) определите скорость велосипедиста в момент времени t = 3 с.

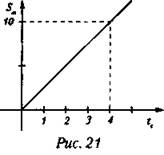
А. 4 м/с.

Б. 10 м/с.

В. 40 м/с.

Г. 2,5 м/с.

6. На рис. 22 представлены три графика зависимости пройденного пути от времени. Какое из тел двигалось с меньшей скоростью?

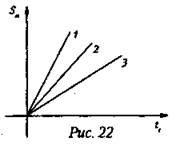
А. 1.

Б. 2.

В. 3.

Г. Скорости всех трех тел одинаковы.

7. Поезд длиной 200 м въезжает на мост со скоростью 5 м/с. За сколько времени поезд пройдет весь мост, если длина моста 300 м?

А. 20 с.

Б. 40 с.

В. 60 с.

Г 100 с.

8. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми по модулю скоростями, равными 20 м/с. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км?

А. 75 с.

Б. 88 с.

В. 150 с.

Г. 300 с.

9. Лестница, приставленная к вертикальной стене, падает в результате скольжения ее основания по полу (рис. 23). Каково отношение модулей скоростей V_A и V_B в тот момент, когда угол между лестницей и стеной равен α?

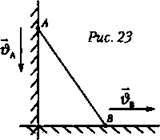
A. sin α.

Б. cos α.

В. tg α.

Г. ctg α.

10. Автомобиль затратил на прохождение пути время t. Первую половину времени автомобиль проходил с постоянной скоростью 20 м/с, а вторую половину времени - со скоростью 30 м/с, двигаясь в том же направлении. Чему равна средняя скорость автомобиля?

А. 25 м/с.

Б. 24 м/с.

В. 10 м/с.

Г. 50 м/с.

Ответ:

Вариант 1: 1. 2. В. 3. Г. 4. В. 5. А. 6. А. 7. Г. 8. А. 9. В. 10. В

Вариант 2: 1. В. 2. Г. 3. Б. 4. В. 5. Г. 6. В. 7. Г. 8. В. 9. В. 10. А

Данную самостоятельную работу можно провести в начале следующего урока.

Домашнее задание

Задачи на с. 24 (3, 4).