Динамика свободных колебаний - ЗАКОНЫ СОХРАНЕНИЯ - Поурочные разработки по физике к учебнику С. В. Громова - Физика - Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс - разработки уроков - авторские уроки - план-конспект урока

ЗАКОНЫ СОХРАНЕНИЯ

Урок 4. Динамика свободных колебаний

Цель: выяснить, от чего зависят свободные колебания пружинного маятника.

Ход урока

I. Изучение нового материала

Механические колебания - это движения, которые точно или приблизительно повторяются через определенный интервал времени.

Вынужденные колебания - это колебания, которые происходят под действием внешней, периодически изменяющейся силы. (Движение иглы швейной машины.)

Свободные колебания - это колебания, которые происходят в системе под действием внутренних сил, после того, как система была выведена из состояния равновесия. (Колебания маятника часов, качели.)

Эксперимент

Демонстрация колебательных систем: пружинный маятник, колебание натянутой веревки, математический маятник, канонический маятник, движение жидкости в U-образной трубке.

- Что общего у всех колебательных систем?

Условия возникновения механических колебаний:

1. Наличие положения устойчивого равновесия, при котором равнодействующая равна нулю.

2. Хотя бы одна сила должна зависеть от координат.

3. Наличие в колеблющейся материальной точке избыточной энергии.

4. Если тело вывести из положения равновесия, то равнодействующая не равна нулю.

5. Силы трения в системе малы.

Рассмотрим движение тележки массой m, прикрепленной к вертикальной стенке пружиной жесткостью R.

При растяжении пружины на х₀ = А (амплитуда) на тело начинает действовать сила упругости, которая стремится вернуть тело в положение равновесия, но, дойдя до положения равновесия, в котором сила упругости равна нулю, тело начинает сжимать пружину, при сжатии пружины появляется возвратная сила упругости, направленная к положению равновесия.

Демонстрация. На тележку прикреплен фломастер, под тележку положен кусок ватмана. Выведем тележку из положения равновесия и одновременно будем двигать ватман на себя. Что же увидим?

Увидим линию, т. к. тележка движется, значит, изменяется координата. Линия будет выражать зависимость координаты от времени. На ватмане будет косинусоида.

Свободные колебания пружинного маятника являются гармоническими.

Зависимость координаты от времени можно записать так:

где А или X_м - амплитуда - максимальное отклонение от положения равновесия. Так как косинус изменяется от -1 до 1, то координата лежит в промежутке:

-А ≤ x ≤ А.

Такой величиной может быть не обязательно координата давления, но сила тока и т. д. w₀ - циклическая частота. Найдем период по II закону Ньютона:

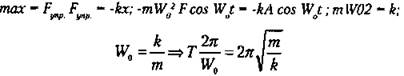
Период определяется жесткостью пружины, и малой, т. е. собственными характеристиками колебательной системы.

Далее учащиеся открывают с. 173 и читают об энергии свободных колебаний, затем отвечают на вопрос:

- Как полная механическая энергия гармонических колебаний зависит от их амплитуды?

Фронтальный эксперимент

Оборудование: держатели на пружинах, штативы, секундомер или метроном, наборы грузов.

1. Соберите пружинный маятник.

2. Измерьте его период.

3. Зная массу груза, рассчитайте жесткость пружины.

4. Полученный результат проверьте по закону Гука.

II. Решение задач

1. Координата колеблющегося тела изменяется по закону: х = 5 cos πt. Чему равна амплитуда, период и частота колебаний, если в формуле все величины выражены в единицах СИ?

Дано:

х = 5 cos πt.

А - ?

Т - ?

V - ?

Решение:

Сопоставим данный закон изменения координаты с законом гармонических колебаний.

Видно, что множитель А перед косинусом есть амплитуда колебаний, следовательно, амплитуда колебаний тела равна 5 м, так как в данном законе этот множитель равен 5. Множитель перед временем t под знаком косинуса в обеих формулах одинаков, поскольку данное движение тела является также гармоническим колебанием. Поэтому

Частоту колебаний найдем по формуле:

(Ответ: А = 5 м; Т = 2 с; х = 0,5 Гц.)

2. Уравнение движения гармонического колебания имеет вид х = 0,02 cos π/2t. Найти координаты тела через 0,5 с; 2 с. Все величины в формуле выражены в единицах СИ.

3. Напишите закон гармонического колебания груза на пружине, если амплитуда колебаний 80 см, а частота колебания - 0,5 Гц.

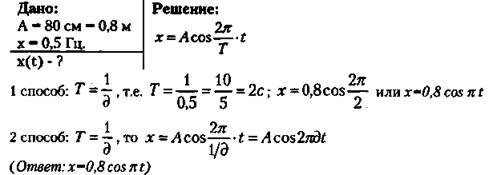
4. Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

(Ответ: А = 0,3 м; Т - 1,6 с; х = 0,625 Гц; x(t) = 0,3 cos 1,25 πt, х₁ ≈ 0,28 м; х₂ ≈ 0,21 м.)

Домашнее задание

П. 37. задачи на с. 327 (169-172).