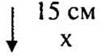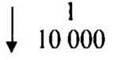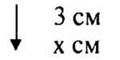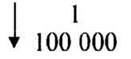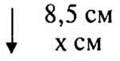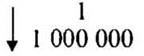Поурочные разработки по Математике 6 класс
Масштаб - ОТНОШЕНИЯ И ПРОПОРЦИИ - ОБЫКНОВЕННЫЕ ДРОБИ
Цели: ввести понятие масштаба; учить читать масштаб; решать задачи, связанные с понятием масштаба.
Информация для учителя
Задачи, связанные с понятием масштаба, показывают одно из практических применений понятия отношения.
Ход урока
I. Организационный момент
II. Анализ контрольной работы
1. Сообщить результаты контрольной работы.
2. Решить задания, вызвавшие затруднения у учащихся.
III. Устный счет
1. Выразите в километрах:
а) 32 000 000 см; б) 600 000 см; в) 32 000 см; г) 5 000 000 см.
— Что нужно сделать, чтобы выразить данные величины в км? (Так как 1 км = 100 000 см, то нужно разделить на 100 000.)
2. Выразите в метрах:
а) 32 000 000 см; б) 600 000 см; в) 32 000 см; г) 5 000 000 см.
IV. Индивидуальная работа
1 карточка
1. Решить уравнение: 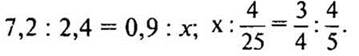
2. На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?
2 карточка
1. Решить уравнение: 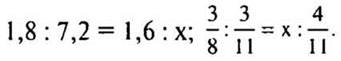
2. Для перевозки угля автомашине грузоподъемностью 6 т надо сделать 10 рейсов. Сколько придется сделать рейсов автомашине, грузоподъемность которой на 2 т меньше, чтобы перевезти этот груз?
V. Сообщение темы урока
— Сегодня мы познакомимся с масштабом. Именно понятие масштаба показывает нам практическое применение отношений.
VI. Изучение нового материала
1. Подготовительная работа.
— Составьте отношения: а) 1 см к 4000 м; б) 1 см к 120 м; в) 1 см к 10 000 км; г) 1 см к 25 см.
— Что нужно сначала сделать? (Перевести в одинаковые единицы измерения.)
— Давайте все величины запишем в сантиметрах.
Решение:
а) 1 : 400 000; б) 1 : 12 000; в) 1 : 1 000 000 000; г) 1 : 25.
— Мы с вами знаем, что участки земной поверхности, детали машин и многое другое изображают на бумаге в уменьшенном виде.
— Если на карте, плане или чертеже встретите такие отношения, то это масштаб карты, плана или чертежа.
2. Работа над новой темой.
Определение. Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты. Аналогично можно сказать о чертеже или плане.
Масштаб — желз размерный или мерило, мерник, размерник, мера линейная, принятая для чертежа или иной работы. (Из толкового словаря В. И. Даля.)
— Объясните, что обозначают данные масштабы.
Задание: а) проговаривает учитель, дальше учащиеся объясняют по нескольку раз один и тот же масштаб.
Ответ:
а) Если масштаб карты 1 : 400 000, то на этой карте длина каждого отрезка уменьшена в 400 000 раз. На такой карге расстояние, равное 4 км, будет изображаться отрезком в 1 см.
Масштаб карты 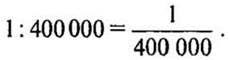 Говорят, что карта сделана в масштабе одна четырехсоттысячная.
Говорят, что карта сделана в масштабе одна четырехсоттысячная.
б) Если масштаб карты 1 : 12 000, то на этой карте длина каждого отрезка уменьшена в 12 000 раз. На такой карте расстояние, равное 120 м, будет изображаться отрезком в 1 см.
Масштаб карты  Говорят, что карта сделана в масштабе одна двенадцатитысячная.
Говорят, что карта сделана в масштабе одна двенадцатитысячная.
3. Работа с учебником.
— Самостоятельно разберите задачу 1 на стр. 134.
— Составьте похожую задачу.
Задача. Длина отрезка на карте 15 см. Найдите длину соответствующего отрезка на местности, если масштаб карты 1 : 10 000.
— Что означает масштаб 1 : 10 000?
— Давайте ее решим, оформив краткую запись в виде таблицы.
Решение:
Пусть х (м) — расстояние на местности.
Расстояние |
Масштаб |
|
На карте На местности |
|
|
15 : х = 1 : 10 000
х = 150 000
150 000 см = 1500 = 1,5 км
(Ответ: 1,5 км расстояние на местности.)
VII. Физкультминутка
VIII. Закрепление изученного материала
1. Практическая работа.
№ 820 стр. 134 (под руководством учителя).
— Прочитайте задание. Можем сразу найти расстояние?
— Что нужно знать сначала? (Длину отрезка на карте.)
— Как узнать длину отрезка на карте? (Измерить по карте с помощью линейки.)
— Измерьте расстояние на карте. Что означает масштаб 1 : 100 000? (1 см на карте равен 100000 см или 1000 м или 1 км на местности.)
— Запишем решение.
Решение:
Пусть х м — расстояние на местности.
Расстояние |
Масштаб |
|
На карте На местности |
|
|
3 : х = 1 : 100 000
х = 300 000
300 000 см = 3000 м = 3 км
(Ответ: 3 км - расстояние на местности.)
2. Работа над задачей.
№ 821 стр. 134.
— Прочитайте задачу.
— Что известно? Что надо узнать?
— Что означает данный масштаб? (1 см на карте равен 1 000 000 см, или 10 000 м, или 10 км на местности.)
Решение:
Пусть х м — расстояние на местности.
Расстояние |
Масштаб |
|
На карте На местности |
|
|
8,5 : х = 1 : 1 000 000
х = 8,5 · 1 000 000
х = 8 500 000
8 500 000 см = 85 км
(Ответ: 85 км на местности.)
IX. Работа над задачей
№ 835 стр. 136 (один ученик решает на обратной стороне доски, остальные — в тетрадях, самопроверка).
— Прочитайте задачу.
— Составьте краткую запись.
— Решите самостоятельно задачу, составив пропорцию.
Решение:
Пусть х кг — картофеля для 12 порций.
Количество порций |
Масса картофеля |
|
1 раз 2 раз |
4 п. 12 п. |
0,44 кг х кг |
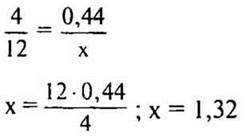
1,32 кг - картофеля для 12 порций.
(Ответ: 1,32 кг.)
— Кто закончил раньше, помогите товарищу, который с помощью сигнальной карточки зовет вас на помощь.
X. Тест (7 мин)
Вариант I
1. Какая из пропорций верна: а) 2 : 6 = 5 : 15; б) 7 : 8 = 3 : 4; в) 7 : 14 = 8: 15.
2. Неизвестный член пропорции 24 : х = 12 : 4
а) х = 5; б) х = 8; в) х = 11.
3. Неизвестный член пропорции: 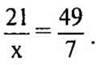
а) х = 12; б) х = 8; в) х = 3.
Вариант II
1. Какая из пропорций верна: а) 5 : 7 = 10 : 15; б) 4 : 7 = 8 : 14; в) 4 : 7 = 7 : 15.
2. Неизвестный член пропорции 28 : х = 36 : 9
а) х = 7; б) х = 9; в) х = 6.
3. Неизвестный член пропорции: 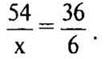
а) х = 5; б) х = 9; в) х = 8.
XI. Подведение итогов урока
— Что называют масштабом карты?
— Где в практической деятельности человек пользуется этим понятием?
— Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? Уменьшены в 50 раз?
Домашнее задание
№ 842, 844, 846 (а) стр. 137. По желанию № 840 стр. 137.