Наибольший общий делитель. Взаимно простые числа - урок 2 - ДЕЛИМОСТЬ ЧИСЕЛ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: обобщить имеющиеся у учащихся знания о наибольшем общем делителе натуральных чисел, о взаимно простых числах; развивать умение самостоятельно работать: воспитывать умение внимательно выслушивать мнение других.

Ход урока

I. Организационный момент

II. Устный счет

— Может ли разложение на простые множители числа 14 652 содержать множитель 3? Почему? (Сумма цифр числа равна 18, 18 делится на 3, значит, данное число делится на 3.)

— Назовите все нечетные числа, удовлетворяющие неравенству 234 < x < 243.

— Назовите 3 числа, кратных: а) 5; б) 15; с) числу а.

— Назовите по 3 числа, взаимно простых с числом: 3, 7, 10, 24.

3: 5, 7, 8;

7: 12,24,43;

10: 3, 7, 13;

24: 7, 13, 17.

— Петух, стоя на одной ноге, весит 5 кг. Сколько он будет весить, если встанет на обе ноги? (5 кг.)

III. Индивидуальная работа

1 карточка

1. Запишите два простых числа х, которые удовлетворяют неравенству 11 < х < 22.

2. Докажите, что числа 136 и 119 не взаимно простые.

3. Разложите на простые множители 252.

4. Найдите наибольший общий делитель:

а) 35 и 18; б) 36, 54 и 72.

2 карточка

1. Запишите два простых числа х, которые удовлетворяют неравенству 21 < х < 37.

2. Докажите, что числа 209 и 171 не взаимно простые.

3. Разложите на простые множители 226.

4. Найдите наибольший общий делитель:

а) 49 и 48; б) 12, 18 и 20.

IV. Сообщение темы урока

— Сегодня на уроке мы продолжим находить наибольший общий делитель натуральных чисел и будем решать задачи.

V. Закрепление изученного материала

1. Один ученик работает у доски, остальные — в тетрадях.

Найдите наибольший общий делитель числителя и знаменателя дробей.

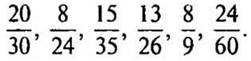
Сначала проверьте, не будет ли большее число делиться на наименьшее из них число. Если да, то меньшее число и есть их наибольший общий делитель.

Ответ: НОД (20; 30) = 10, НОД (8; 24) = 8, НОД (15; 35) = 5, НОД (13; 26) = 13, НОД (8; 9) = 1, НОД (24; 60) = 12.

2. Устно докажите, что числа взаимно простые:

а) 7 и 13; б) 25 и 64; в) 12; 6 и 5.

VI. Физкультминутка

VII. Работа над задачей

1. № 153 стр. 26 (самостоятельно в тетрадях).

— Прочитайте задачу.

— Запишите решение.

— Кто не знает, как решать эту задачу, подойдите к доске.

2. Индивидуальная работа. (Учитель подробно разбирает задачу.)

— О ком говорится в задаче?

— О чем говорится в задаче?

— Расскажите задачу.

— Назовите первую часть вопроса задачи. (Сколько автобусов было выделено?)

— Можно сразу узнать, сколько автобусов было выделено? (Нет. Мы не знаем, сколько пассажиров в каждом автобусе.)

— Назовите вторую часть вопроса задачи. (Сколько пассажиров было в каждом автобусе?)

— Как это узнать? (Найти НОД чисел 424 и 477.)

Решение:

1) НОД (424; 477) = 53, значит, 53 пассажира в одном автобусе.

2) 424 : 53 = 8 (авт.) - в лес.

3) 477 : 53 = 9 (авт.) — на озеро.

4) 8 + 9 = 17 (авт.)

— Как по-другому можно найти количество автобусов? (Узнать, сколько всего пассажиров было, и общее количество пассажиров разделить на количество пассажиров в одном автобусе.)

424 + 477 = 901 (п.) — всего.

901 : 53 = 17 (авт.).

(Ответ: всего автобусов 17; в каждом автобусе 53 человека.)

3. № 165 (1) стр. 28.

— Прочитайте задачу.

— Что известно? Что надо найти? Составьте краткую запись.

Решение:

1) 820 : 5 · 2 = 328 (м) — отремонтировали во вторник.

2) 820 — 328 = 492 (м) — осталось отремонтировать.

3) 492 : 3 · 2 = 328 (м) — отремонтировали в среду.

4) 492 — 328 = 164 (м) — отремонтировали в четверг.

(Ответ: 164 м.)

VIII. Повторение изученного материала

1. Пока те учащиеся, которые разбирали задачу у доски, записывают решение, остальные выполняют № 154 стр. 26.

— Запишите промежуточные ответы.

Ответ:

а) 7; 3,5; 3,2; 8

б) 0,5; 0,1; 2,1; 3

в) 3,2; 4; 0,4; 0,2

г) 0,96; 3,2; 3; 0,3

д) 0,3; 1,5; 0,1; 10.

2. № 155 стр. 27 (устно).

— Так как расстояние от 5 до а, от а до с равно расстоянию от 0 до 5, следовательно, а = 10, с = 15, значит а, с — составные числа.

— Так как расстояние от 0 до в равно пяти расстояниям от 0 до 5 да еще 1 единичный отрезок, то в = 26, значит в - составное.

3. № 163 стр. 27 (взаимопроверка).

— Определите вид углов. (Угол ЛОВ - острый, угол DEF — тупой.)

IX. Историческая справка

— Где возникло градусное измерение углов? (В Древнем Вавилоне.)

— Еще Клавдий Птолемей (II в.) использовал в своих трудах единицы измерения углов: градус, минута, секунда. Как он их обозначал? (Как и мы сейчас обозначаем.)

X. Самостоятельная работа (10 мин)

Вариант I

1. Найдите все общие делители чисел и подчеркните их наибольший общий делитель: а) 50 и 70; б) 34 и 51; в) 8 и 27.

Назовите пару взаимно простых чисел, если такая пара есть.

2. Запишите два числа, для которых наибольшим общим делителем будет число: а) 7; б) 24.

3. Найдите наибольший общий делитель данных чисел: а) 55 и 88; б) 72 и 96; в) 720 и 90; г) 15; 25; 35.

Вариант II

1. Найдите все общие делители чисел и подчеркните их наибольший общий делитель: а) 30 и 40; б) 39 и 65: в) 25 и 9.

Назовите пару взаимно простых чисел, если такая пара есть.

2. Запишите два числа, для которых наибольшим общим делителем будет число: а) 9; б) 21.

3. Найдите наибольший общий делитель данных чисел: а) 44 и 99; б) 630 и 70; в) 64 и 80; г) 15; 27; 33.

Решение:

Вариант I

1. а) 50: 1, 2, 5, 10, 25, 50; 70: 1, 2, 5, 7, 10, 14, 35, 70;

50 и 70: 1, 2, 5, 10.

б) 34: 1, 2, 17, 34; 51: 1, 3, 17, 51;

34 и 51: 1, 17.

в) 8: 1, 2, 4, 8; 27: 1, 3, 9, 27;

8 и 27: 1.

8 и 27 — взаимно простые числа.

2. а) 7 = НОД (14; 21); б) 24 = НОД (24; 72).

3. а) НОД (55; 88) = 11; б) НОД (72; 96) = 24; в) НОД (720; 90) = 90; г) НОД (15; 25; 35) = 5.

Вариант II

1. а) 30: 1, 2, 3, 5, 6, 10, 15, 30; 40: 1, 2, 4, 5, 8, 10, 20, 40;

30 и 40: 1, 2, 5, 10.

б) 39: 1, 3, 13, 39; 65: 1, 5, 13, 65;

39 и 65: 1, 13.

в) 25: 1, 5, 25; 9: 1, 3, 9;

25 и 9: 1.

25 и 9 — взаимно простые числа.

2. а) 9 = НОД (45; 81); б) 21 = НОД (21; 63).

3. а) НОД (44; 99) = 11; б) НОД (630; 70) = 70; в) НОД (64; 80) = 16; г) НОД (15; 27; 33) = 3.

XI. Подведение итогов урока

— Если числа взаимно простые, то какому числу равен их наибольший общий делитель?

— Верно ли: «Если числа простые, то они взаимно простые»? Ответ обоснуйте. (Да, так как простые числа имеют только два делителя: 1 и само число, следовательно, наибольшим общим делителем всех данных чисел будет 1.)

Домашнее задание

№ 175-177, 178 (б) стр. 29.

Можно предложить самостоятельно изучить параграф 7 на стр. 29—30 в учебнике.