Поурочные разработки по Математике 6 класс
Решение уравнений - урок 4 - РЕШЕНИЕ УРАВНЕНИЙ - РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели: отрабатывать навык решения уравнений, основанный на использовании их свойств, задач с помошью уравнений; обобщить и закрепить знания по теме «Решение уравнений»; подготовить учащихся к контрольной работе.
Ход урока
I. Организационный момент
II. Устный счет
1. Упростите: 1) 2х + 3х; 2) -2х + 3х; 3) 2х - 3х; 4) -2х - 3х;
2. Решите уравнение: 1) (х — 7)(х + 4) = 0; 2) |х + 4| = 0; 3) |х — 7| = 1; 4) х — 7 = 1; 5) 7х = 1; 6) 7х = 0.
3. При решении уравнения ax = b, где х — неизвестное число, коэффициент а оказался стертым. Восстановите его.
1) ...х = —12; х = —4.
2) ...х = 18; х = 9.
3) ...х = —25; х = 5.
4) ...х = 24; х = —4.
4. С одной яблони собрали 12 кг яблок, с другой в 2 раза больше. Яблоки разложили поровну в 6 корзин. Сколько килограммов яблок в каждой корзине?
5. Мама купила торт «Птичье молоко» весом 600 г.
Как разрезать торт на части, чтобы его можно было разделить поровну и на троих, и на четверых человек? Постарайтесь сделать как можно больше кусков.
Решение:
Разрежем сначала торт на четыре части по 150 г.
Затем одну четвертую часть разрежем на три части по 50 г. Имеем: 600 = 150 + 150 + 150 + 150 + 50 + 50 + 50, т. е. торт можно разделить поровну и на троих по 200 г, и на четверых по 150 г.
(Ответ: на троих по 200 г и на четверых по 150 г.)
III. Индивидуальная работа
1 карточка
Решить уравнения:
1. -2х + 4 = 3х - 21;
2. 4х + 3 = -16;
3. -5х + 9 = 2х + 3;
4. 3х + 4 = -х - 12;
5. 4х - (3 - 2х) = - (13 - 5х).
2 карточка
Решить уравнения:
1. -3х + 2 = 5х - 15;
2. 2х + 7 = —19;
3. -4х + 7 = 5х + 1;
4. 4х + 3 = -2х - 5;
5. 2х - (4 - 5х) = - (6 - 3х).
IV. Сообщение темы урока
— Сегодня на уроке мы будем готовиться к контрольной работе по теме «Решение уравнений».
V. Работа над задачей
№ 1330 стр. 233 (параллельно с разбором записывать решение на доске).
— Прочитайте задачу.
— Каким способом будем ее решать? (Алгебраическим.)
— Как перевести проценты в десятичную дробь?
— Что примем за х? (Первоначальную массу соли в растворе.)
— Зная, что в растворе содержится 40% соли, что можно узнать? (Массу всего раствора.)
— Что значит, соли в растворе будет содержаться 70%?
Решение:
Пусть х (г) — соли первоначально было в растворе.
40% = 0,4
х : 0,4 = 2,5х (г) — первоначальная масса раствора,
х + 120 (г) — соли после того, как ее добавили в раствор,
2,5х + 120 (г) - масса раствора после того, как добавили соль.
70% = 0,7
0,7(2,5х + 120) (г) — соли после того, как ее добавили в раствор.
Составим и решим уравнение:
0,7(2,5х + 120) = х + 120
1,75х + 84 = х + 120
0,75х = 36
х = 48; 48 г - соли первоначально было в растворе.
(Ответ:48 г.)
VI. Физкультминутка
VII. Закрепление изученного материала
1. № 1316 (ж, з) стр. 231 (на обратной стороне доски и в тетрадях, самопроверка).
Решение:

(Ответ: k = 10; с = 2.)
— На чем основано решение этих уравнений?
— Сформулируйте данное свойство уравнения.
2. Решение уравнения (самостоятельно, взаимопроверка).
— Расскажите план решения уравнения.
Решение:
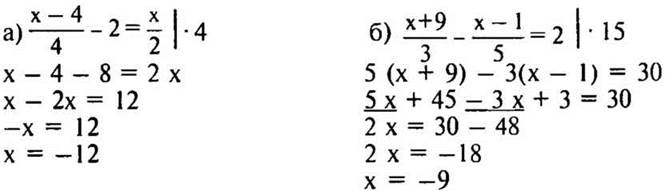
(Ответы: а) х = —12; б) х = —9.)
VIII. Самостоятельная работа (10—15 мин)
Вариант I
1. Решите уравнение:
![]()
2. В пятом и шестом классах учится 70 человек. В пятом классе мальчики составляют 9/20 всех учащихся этого класса, а в шестом классе мальчики составляют 0,6 всех учащихся своего класса. Сколько учащихся учится в пятом классе и сколько учащихся учится в шестом классе, если мальчиков в этих классах поровну?
3. Решите уравнение 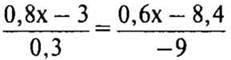 и выполните проверку.
и выполните проверку.
4. В двузначном натуральном числе сумма цифр 6. Число десятков в 2 раза больше числа единиц. Найдите это число.
Вариант II
1. Решите уравнение:
![]()
2. В двух альбомах 1050 марок. В первом альбоме иностранные марки составляют 2/3 всех имеющихся марок, а во втором альбоме иностранные марки составляют 0,5 всех марок этого альбома. Сколько марок в каждом альбоме, если число иностранных марок и в том, и в другом альбоме одинаково?
3. Решите уравнение 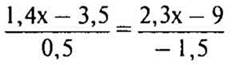 и выполните проверку.
и выполните проверку.
4. В двузначном натуральном числе сумма цифр равна 4, число десятков в 3 раза меньше числа единиц. Найдите это число.
IX. Подведение итогов урока
— Какие свойства уравнений используются при их решении?
— Что значит решить уравнение?
— Что еще мы используем при решении уравнений? (Распределительное свойство умножения при раскрытии скобок, правила раскрытия скобок, если перед скобкой стоит знак «—» или «+», приводим подобные слагаемые.)
Домашнее задание
№ 1342 (к-м), 1341 (в, е) стр. 234, № 1345 стр. 235.