Решение задач - урок 4 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цели: закрепление и проверка знаний и умений учащихся, сформированных при изучении главы XI, формирование навыков решения задач, развитие навыков логического мышления.

Ход урока

I. Математический диктант (10 мин).

Вариант I

1. Вычислите скалярное произведение векторов и , если , а угол между ними равен 120°.

2. Скалярное произведение ненулевых векторов и равно 0. Определите угол между векторами и .

3. Вычислите скалярное произведение векторов и , если (3; –2), (–2; 3).

4. Найдите угол между ненулевыми векторами (х; у) и (–у; х).

5. Вычислите косинус угла между векторами и , если (3; –4), (15; 8).

6. Даны векторы (2; –3) и (х; –4). При каком значении х эти векторы перпендикулярны?

Вариант II

1. Вычислите скалярное произведение векторов и , если , а угол между ними равен 135°.

2. Скалярное произведение ненулевых векторов и равно нулю. Определите угол между этими векторами.

3. Вычислите скалярное произведение векторов и , если (–4; 5), (–5; 4).

4. Найдите угол между ненулевыми векторами (х; –у) и (у; х).

5. Вычислите косинус угла между векторами и , если (–12; 5), (3; 4).

6. Даны векторы (3; у) и (2; –6). При каком значении у эти векторы перпендикулярны?

 

II. Решение задач.

1. Решить задачу № 1025 (б, е, з) на доске и в тетрадях, используя микрокалькулятор.

2. Решить задачу № 1056 на доске и в тетрадях.

Решение

Пусть АВСD – данный ромб. Выразим векторы и через векторы и :

используя эти выражения, получаем: так как АD = АВ. Следовательно, АС ВD, то есть доказали, что диагонали ромба взаимно перпендикулярны.

3. Решить задачу № 1042 на доске и в тетрадях.

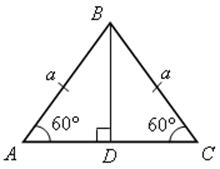
Решение

АВ = ВС = АС = а; ВD АС.

а) cos 60° = a ∙ a ∙ = a2;

б) 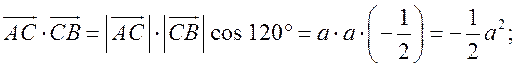cos 120° = cos (180° – 60°) = –cos 60° = –.

в) ∙ cos 90° = 0, так как cos 90° = 0;

г) ∙ cos 0° = a ∙ a ∙ 1 = a2.

ответ: а) a2; б) –a2; в) 0; г) а2.

4. Решить задачу № 1050.

Решение

Скалярный квадрат вектора равен квадрату его длины, тогд.

.

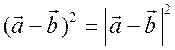52 – 2 ∙ 5 ∙ 8 ∙ + 82 = 25 – 40 + 64 = 49, ; значит, = 7.

Самостоятельно учащиеся находят .

 

III. Устный опрос учащихся по карточкам.

Вариант I

1. Что называется тангенсом угла ? Для какого значения  тангенс не существует и почему?

2. Сформулируйте и докажите теорему синусов.

3. Даны векторы (х; –4) и (2; 3). Найдите значение х, если .

Вариант II

1. Напишите формулы приведения.

2. Сформулируйте и докажите теорему косинусов.

3. Найдите скалярное произведение векторов (–5; 7) и (2; 1).

Вариант III

1. Что такое скалярное произведение векторов?

2. Сформулируйте и докажите теорему о вычислении площади треугольника по двум сторонам и углу между ними.

3. Найдите косинус угла А треугольника АВС, если АВ = 8 см, АС = 6 см, ВС = 12 см.

Вариант IV

1. Какие два вектора называются перпендикулярными?

2. Выведите формулу, выражающую косинус угла между ненулевыми векторами через их координаты.

3. Найдите синус угла В треугольника АВС, если АВ = 5 см, АС = 8 см, С = 30°.

 

IV. Итоги уроков.

Домашнее задание: подготовиться к контрольной работе, повторить материал пунктов 93–104; решить задачи №№ 1065, 1068, 1060 (а, б), 1061 (а, б).