Угол между векторами. Скалярное произведение векторов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цели: познакомить учащихся с понятием угла между векторами; ввести скалярное произведение векторов; рассказать о применении скалярного произведения векторов в физике, механике; развивать логическое мышление учащихся.

Ход урока

I. Математический диктант (15 мин).

Вариант I

1. Диагонали параллелограмма АВСD пересекаются в точке О. какие векторы коллинеарные вектору ?

2. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы сонаправлены с вектором ?

3. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что = 3, = 4. Найдите , если АОВD – прямоугольник.

6. В треугольнике СDЕ DЕ = 5, СЕ = 4, угол С = 45°. Найдите сторону DЕ.

7. В треугольнике КLM КL = LМ = 5, КМ = 6. Найдите косинус угла L.

8. В треугольнике ОРQ угол О = 60°, угол Р = 75°, ОР = 8. Найдите сторону РQ.

Вариант II

1. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы коллинеарные вектору ?

2. Диагонали ромба КLМР пересекаются в точке Т. какие векторы сонаправлены с вектором ?

3. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что точки С и D лежат соответственно на осях ОХ и ОY прямоугольной системы координат. Найдите , если = 5, = 12.

6. В треугольнике АВС АВ = ВС = 8, АС = 4. Найдите косинус угла А.

7. В треугольнике ВСD ВС = 6, угол В = 75°, угол С = 45°. Найдите сторону ВD.

8. В треугольнике DЕF DЕ = 6, ЕF = 7, угол Е = 30°. Найдите сторону DF.

II. Объяснение нового материала.

1. Ввести понятие угла между векторами и (рис. 300 и таблица).

2. Угол  между векторами и не зависит от выбора точки О, от которой откладываются векторы и .

3. Угол между сонаправленными векторами считается равным нулю.

4. Обозначение угла между векторами: .

5. Определение углов между векторами на рисунке 301.

6. Определение перпендикулярных векторов.

7. Повторить по настенным таблицам сложение и вычитание векторов, умножение вектора на число.

8. Введение еще одного действия над векторами – скалярного умножения векторов. В отличие от суммы и разности векторов скалярное произведение есть число (скаляр) – именно это и обусловило название операции.

9. В тетрадях учащиеся оформляют таблицу:

скалярное произведение векторов

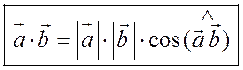
Если и , т.

а) (0 ≤ < 90°) <=> ( > 0); б) (90° < ≤ 180°) <=> (< 0);

в) <=> ( = 0); г) (= 0°) <=> .

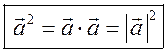
10. Скалярное произведение векторов широко используется в физике. Например, из курса механики известно, что работа А постоянной силы при перемещении тела из точки М в точку N (рис. 303) равна произведению длин векторов силы и перемещения на косинус угла между ними: .

III. Закрепление изученного материала.

1. Решить задачи №№ 1039 (а, б, ж, з) и 1040 (а, д, е) по готовым чертежам квадрата и ромба, заранее выполненным на доске.

2. Решить задачу № 1041 (в).

Примечание. сos 135° = cos (180° – 45°) = – cos 45° = .

IV. Итоги урока.

Домашнее задание: изучение материалов пунктов 101 и 102; повторить материал п. 87; решить задачи №№ 1039 (в, г), 1040 (г), 1042 (а, б).