Уроки-конспекты по Геометрии 8 класс
ПРИМЕНЕНИЕ ПОДОБИЯ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ И РЕШЕНИЮ ЗАДАЧ - урок 4
Цель: закрепить изученный материал при решении задач.
Ход урока
I. Проверка домашнего задания.
1. Выполнить задание (устно): найдите неизвестные элементы прямоугольного треугольника:
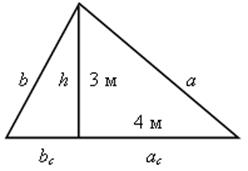
![]() (м).
(м).
![]() .
.
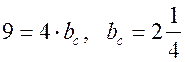 (м).
(м).
 (м).
(м).
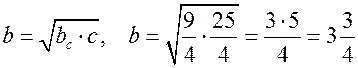 (м).
(м).
2. Рассмотреть решение задачи № 576.
II. Решение задач.
1. № 577.
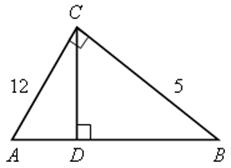
Решение
Треугольник является прямоугольным, так как в нем выполняется теорема Пифагора: 132 = 122 + 52.
2) Пусть DВ = х см, тогда
СВ2 = DВ · АВ; 25 = х · 13, х = 1![]() (см).
(см).
АD = АВ – DВ = 13 – 1![]() = 11
= 11![]() (см).
(см).
2. Решить (устно): АА1 || ВВ1 || СС1. Найти х и у.
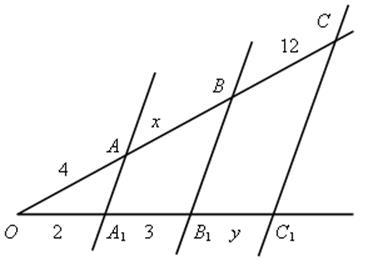
3. № 384. Решена в учебном пособии, с. 149.
4. № 585 (а).
5. № 614.
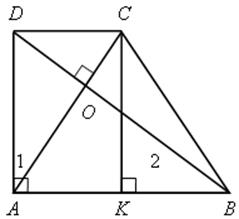
Решение
1) ![]() АОD
АОD ![]()
![]() ВАD, поэтому
ВАD, поэтому ![]() 1 =
1 = ![]() 2, тогда
2, тогда
2) ![]() АDС
АDС ![]()
![]() ВАD
ВАD
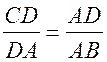 ; CD =
; CD =  = 2
= 2![]() (см).
(см).
3) ![]() АВD,
АВD, ![]() А = 90°, по теореме Пифагора: ВD =
А = 90°, по теореме Пифагора: ВD = ![]() =
= ![]() (см).
(см).
4) ![]() ВСK,
ВСK, ![]() K = 90° по теореме Пифагора
K = 90° по теореме Пифагора
ВС = 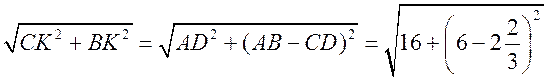 =
= 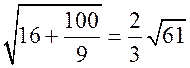 (см).
(см).
III. Итоги урока.
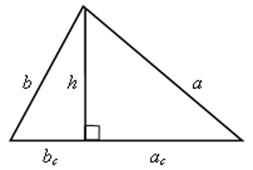
![]()
![]()
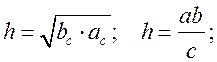
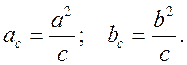
Домашнее задание: №№ 585 (в), 607, 623; подготовиться к самостоятельной работе.
№ 623. (Комментарий учителя обязателен.)
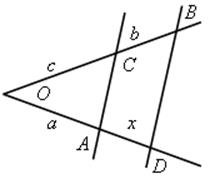
Воспользоваться задачей № 556.
Пусть ОА = а; ОС = с; ВС = b. АС || ВD, АD – искомый отрезок.
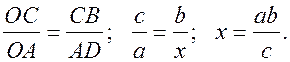
Для желающих.
Доказать, что в прямоугольном треугольнике квадрат медианы, проведенной к катету, равен разности квадрата гипотенузы и трех четвертей квадрата соответствующего медиане катета.
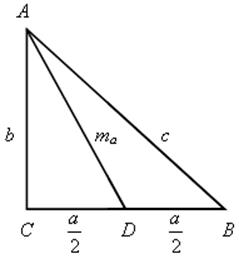
Решение
1) В ![]() АСD,
АСD, ![]() С = 90°, по теореме Пифагора
С = 90°, по теореме Пифагора 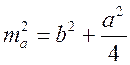 ;
;
2) в ![]() АСВ по теореме Пифагора b2 = c2 – a2;
АСВ по теореме Пифагора b2 = c2 – a2;
3) Имеем 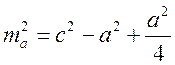 ;
; 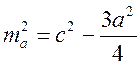 .
.