ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ТРЕУГОЛЬНИКА И ТРАПЕЦИИ - урок 4

Цели: доказать теорему о площади трапеции; познакомить учащихся с методами решения задач по этой теме.

Ход урока

I. Проверка домашнего задания.

№ 469.

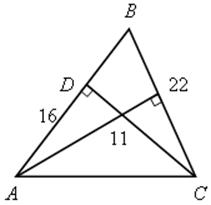
SАВС = AB ∙ CD,

SАВС = 16 ∙ 11 = 88 (см2),

SАВС = BC ∙ h,

88 = ∙ 22 ∙ h,

h = 8 (cм).

№ 472.

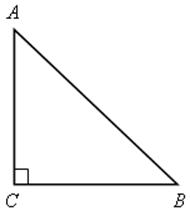
SАВС = 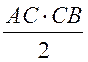, так как .

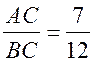АС = 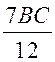, 168 = 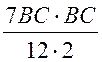, ВС2 = 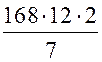, ВС2 = 24 · 24, ВС = 24 см, АС = 14 см.

№ 479 (а).

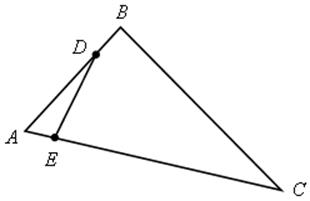
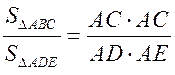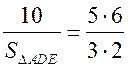, , SАDE = 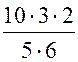= 2 (см2).

II. Объяснение нового материала.

Доказательство теоремы о площади трапеции можно предложить учащимся разобрать самостоятельно.

III. Закрепление изученного материала.

Решить задачу.

Дано: S = 18 см2, а = 2 см, b = 7 см.

Найти: h.

Ответ: h = 4 cм.

№ 480 (в).

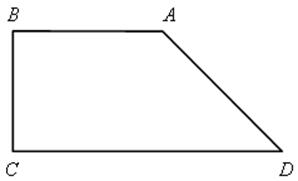
Решение

SАВСD = 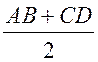∙ BC, SАВСD = 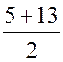∙ 8, SАВСD = 72 (см2).

№ 481.

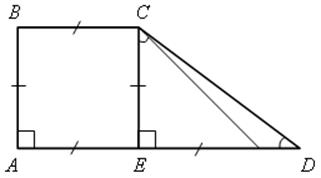
Решение

ВСD = 135°, ВСЕ = 90°,

ЕСD = 45°, СDЕ = 45°.

Имеем СDЕ – равнобедренный, то есть СЕ = ЕD.

Четырехугольник АВСЕ – квадрат, поэтому АВ = СЕ = ВС = АЕ.

SАВСD = 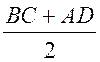∙ AB = 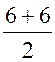∙ 6 = 36 (см2).

№ 482.

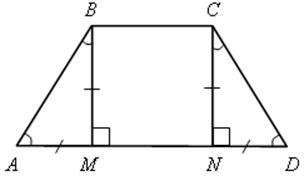
Решение

ВСD = 135°, NСL = 45°,

NСD = СDN = 45° NС = ND = 1,4 см;

МN = AN – MN = 3,4 – 1,4 = 2 (см);

МN = ВС.

SАВСD = 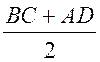∙ NC = 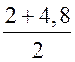∙ 1,4 = 4,76 (см2).

IV. Итоги урока.

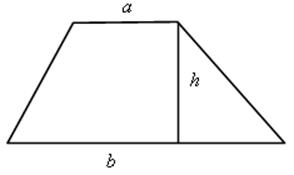
Sтрапеции =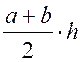

Домашнее задание: § 2, вопрос 7, с. 134; №№ 480 (8), 518 (а).

Для желающих.

В трапеции АВСD, АD – большее основание, D = 60°. Биссектрисы углов С и D пересекаются в точке 0, ОD = а, ВС = b, АD = с.

Найдите площадь трапеции.

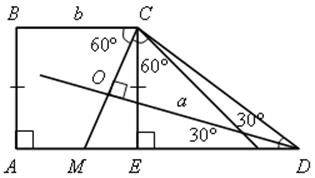
Решение

СDЕ – равносторонний, так как МСD = СDМ = СМD = 60°.

СМ = ОD, то есть ОD – высота МСD.

В равностороннем треугольнике высоты равны.

SАВСD = 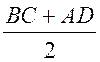∙ OD = 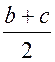∙ a.