Простейшие задачи в координатах. Контрольная работа № 1 - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- закрепление навыков учащихся в использовании формул для решения задач координатно-векторным методом;

- контроль знаний и умений.

Ход урока

I. Организационный момент

Сообщить учащимся тему и цели урока.

II. Актуализация опорных знаний

Проверка домашнего задания (форме фронтальной беседы с учащимися).

1. Какие виды треугольников получились в задании № 431? (Ответ: а) равносторонний; в) прямоугольный; г) прямоугольный.)

Какие теоретические сведения использовались при решении этого задания?

2. Какие случаи рассмотрели в № 435? (Ответ: АВ = ВС и АС = ВС, АВ = АС.)

3. Ответы заданий II уровня:

Задача № 437 (Ответ: а) (-1,6; 0; 0); б) (0; 8; 0); в) (0; 0; 1).)

Какие формулы использовались?

Дополнительная задача.

(Ответ: m = 2; n = 6.)

III. Формирование навыков и умений учащихся

1. Решить задачу № 438 (а).

Дано: А(-1; 2; 3), В(-2; 1; 2), С(0; -1; 1).

Найти: точку, равноудаленную от этих точек и расположенную на плоскости хОу.

Решение: Пусть точка М - искомая. Так как точка М ∈ хОу, то ZM = 0, то есть М(х; у; 0).

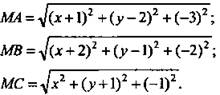
По условию МА = MB = МС. Решим систему: 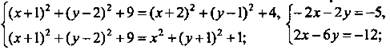(Ответ: .)

Контрольная работа № 1 по теме: «Простейшие задачи в координатах» (20 мин) (см. приложение).

Ответы: I уровень: Вариант I. Вариант II.

Решение задач II уровня.

Вариант I

1) Дано: ΔАВС, А(-2; 0; 1), В(-1; 2; 3), С(8; -4; 9). ВМ - медиана.

Найти: координаты вектора

Решение: По определению медианы, М - середина отрезка АС. Следовательно, координаты М найдем по формулам координат середины отрезка (Ответ: {4; -4; 2}.)

2) Дано:

Найти: координаты вектора .

Решение: По условию коллинеарные, поэтому координаты вектора пропорциональны координатам вектора , то есть По условию составим уравнение: По условию Значит, вектор имеет координаты (Ответ: {-3; 2; 6}.)

3) Дано: А(-1; 5; 3), В(7; -1; 3), С(3; -2; 6).

Доказать: ΔABC - прямоугольный.

Решение: По формуле расстояния между двумя точками найдем длины отрезков АВ, АС, ВС.

Проверим равенство АВ2 = ВС2 + АС2, 100 = 26 + 74 верно.

По теореме обратной теореме Пифагора делаем вывод, что ΔABC - прямоугольный с гипотенузой АВ.

Вариант II

1) Дано: ΔАВС; А(-1; 2; 3), B(1; 0; 4), С(3; -2; 1). AM - медиана.

Найти: координаты вектора

Решение: По определению медианы М - середина ВС.

Координаты точки М найдем по формулам координат середины отрезка. (Ответ: {3; -3; -0,5}.)

2) Дано:

Найти: координаты вектора .

Решение: По условию коллинеарные, поэтому координаты вектора пропорциональны координатам вектора , то есть По условию составим уравнение: По условию Значит, вектор имеет координаты (Ответ: {12; -8; -24}.)

3) Дано: А(-1; 5; 3), В(-1; -3; 9), С(3; -2; 6).

Доказать: ΔAВС - прямоугольный.

Доказательство: По формуле расстояния между двумя точками найдем длины отрезков АВ, АС, ВС.

Проверим равенство АВ2 = АС2 + ВС2. 100 = 76 + 26, верно. По теореме обратной теореме Пифагора делаем вывод, что ΔABC - прямоугольный с гипотенузой АВ.

Решение заданий III уровня.

Вариант I

1) Дано: ΔАВС; М, N, К - середины сторон соответственно АВ, ВС, АС. М(3; -2; 5), N(3,5; -1; 6), К(-1,5; 1; 2).

Найти: координаты А, В, С.

Пусть A (х1; у1; z1), В(х2; у2; z2), С(х3; у3; z3). По формулам координат середины отрезка составим системы для абсцисс, ординат и аппликат.

Пользуясь методом сложения, решим эту систему:

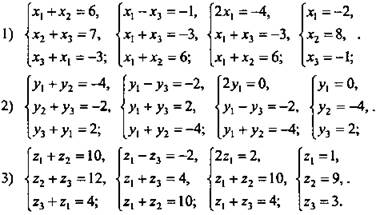
(Ответ: А(-2; 0; 1), В(8; -4; 9), С(-1; 2; 3).)

2) Дано: А(-2; 1; 2), B(-6; 3; -2), С ∈ оси OZ; АС = ВС.

Найти: координаты точки С.

Решение: По условию С ∈ оси OZ, значит она имеет координаты С(0; 0; z) и АС = ВС. Составим уравнение, пользуясь формулой расстояния между двумя точками: (Ответ: (0; 0; -5).)

3) Дано: А(-2; 1; 2), B(-6; 3; -2), С 0; 0; -5); АС = ВС.

Найти: SΔABC.

Решение: По формуле координат середины отрезка АВ найдем координаты точки М — середины: СМ-высота равнобедренного ΔABC. (Ответ: .)

Вариант II

1. Дано: ΔАВС, М, N, К - середины сторон соответственно AB, BС, AС. М(3; -2; -4), N(-6; 4; -10), К(-7; 2; -12).

Найти: координаты вершин А, В, С.

Решение: Пусть A(x1; у1; z1), В (x2; у2; z2), С (x3; у3; z3). По формулам координат середины отрезка составим системы для абсцисс, ординат и аппликат.

При решении системы использован метод сложения.

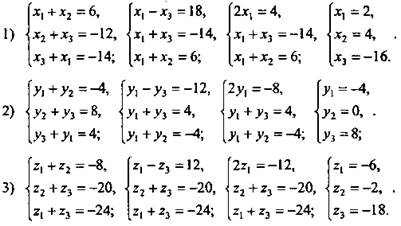
(Ответ: A(2; -4; -6), B(4; 0; -2), С(-16; 8; -18).)

2. Дано: A(4; 5; 4), B(2; 3; -4); С e оси OX, AC = ВС.

Найти: координаты точки С.

Решение: По условию С ∈ оси ОХ, значит она имеет координаты С(х; 0; 0) и АС = ВС. Составим уравнение, пользуясь формулой расстояния между двумя точками: (Ответ: 7; 0; 0.)

3. Дано: А(4; 5; 4), B(2; 3; -4), С(1; 0; 0), АС = ВС.

Найти: SΔABC.

Решение: Пусть точка М - середина основания равнобедренного ΔАВС, то есть отрезка АВ. Тогда точка М имеет координаты: М(3; 4; 0). СМ - высота ΔАВС. (Ответ: 24.)

IV. Подведение итогов

Домашнее задание

I уровень: повторить п. 9, № 438 б), 436, 439 (а);

II уровень: повторить п. 9, № 438 б), 436, 440.

Решение домашнего задания:

Задача № 438 б).

Дано: А(-1; 2; 3), B(-2; 1; 2), С(0; -1; 1), D ∈ (OYZ), AD = BD = CD.

Найти: координаты точки D.

Решение: Точка D имеет координаты D (0; у; z), так как она лежит в плоскости OYZ. Она равноудалена от точек А, В, С, следовательно, 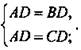По формуле расстояния между точками найдем длины этих отрезков:

Вернемся к системе.

(Ответ: (0; 1; 1,5).)

Задача № 436.

Дано: A(4; 4; 0), В(0; 0; 0), C(0; 3; 4), D(1; 4; 4).

Доказать: ABCD - равнобедренная трапеция.

Решение: По формуле расстояния между двумя точками вычислим стороны четырехугольника ABCD:

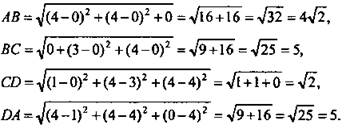
Итак, BC = DA.

Докажем, что AB || СD то есть, что коллинеарные, то есть их координаты пропорциональны. Очевидно, что Значит, коллинеарные, значит, АВ || CD. Итак, АВ || CD и ВС = AD. По определению, четырехугольник ABCD - равнобедренная трапеция.

Задача № 439 а).

Дано: О(0; 0; 0), А(4; 0; 0), В(0; 6; 0), С(0; 0; -2). ΔAОВ - вписанный в окружность W(D; r).

Найти: а) координаты центра окружности D; б) r- радиус окружности.

Решение: Так как точка D - центр описанной окружности, то она равноудалена от вершин треугольника АВО, то есть Из условия задачи видно, что А, О, В, D лежат в одной плоскости, причем, точка О(0; 0; 0) совпадает с началом координат, А(4; 0; 0) лежит на оси Ох; B(0; 6; 0) лежит на оси Оу. Следовательно, ΔАОВ лежит в плоскости хОу и, значит, центр окружности описанной около ΔАОВ лежит в этой же плоскости, то есть D(x; у; О). Решим систему:

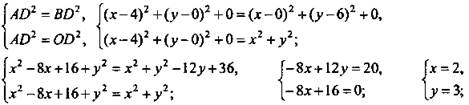
(Ответ: (2; 3; 0); )

Задача № 440.

Дано: ΔАВС - прямоугольный; АС, ВС - катеты; AC = b; BC = a; CD = m; CD ⊥ (ABC); М - середина гипотенузы АВ (рис. 1).

Найти: DM.

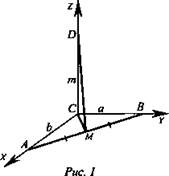
Решение: Введем прямоугольную систему координат с началом в вершине прямого угла С и с осями по катетам: Ох - по катету СА; Оу - по катету СВ, а точка D будет лежать на оси Oz. Координаты данных точек: А(b; 0; 0), B(0; а; 0), С(0; 0; 0), D(0; 0; m),

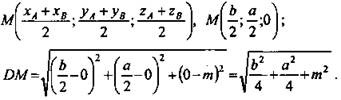(Ответ: )