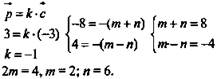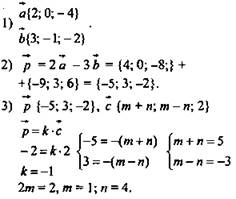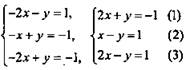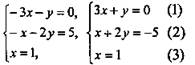Поурочные разработки по Геометрии 11 класс
Простейшие задачи в координатах - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Цели урока:
- вывести формулы координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками;
- показать примеры решения стереометрических задач координатно-векторным методом.
Ход урока
I. Поверка домашнего задания
Проверка домашнего задания осуществляется через кодоскоп. Воспроизводятся решения уровней Б и В.
Уровень Б
№ 419. Дано: ΔABC; А(1; 6; 2), 5(2; 3; -1), С(-3; 4; 5) .
Разложить: ![]() по координатным векторам
по координатным векторам ![]()
Решение:
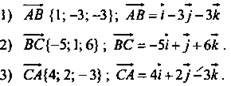
№ 421 а), б).
а) Дано: А(3; -7; 8), В(-5; 4; 1), С(27; -40; 29).
Установить: А; В; С лежат ли на одной прямой.
Решение: Если ![]() коллинеарные, то А; В; С лежат на одной прямой
коллинеарные, то А; В; С лежат на одной прямой ![]()
![]()
![]() - коллинеарные, то есть координаты векторов пропорциональные числа, А, В, С лежат на одной прямой.
- коллинеарные, то есть координаты векторов пропорциональные числа, А, В, С лежат на одной прямой.
б) Дано: А(-5; 7; 12), В(4; -8; 3), С(13; -23; -6).
Установить: А; В; С лежат ли на одной прямой.
Решение: Если ![]() коллинеарные, то А; В; С лежат на одной прямой.
коллинеарные, то А; В; С лежат на одной прямой. ![]()
![]()
![]() - коллинеарные, то есть координаты векторов пропорциональные числа. А; В; С лежат на одной прямой.
- коллинеарные, то есть координаты векторов пропорциональные числа. А; В; С лежат на одной прямой.
Уровень В
№ 422 б). Дано: А(0; 1; 0), В(3; 4; -1), С(-2; -3; 0), D(2; 0; 3)
Установить: А; В; С; D лежат ли в одной плоскости.
Решение: ![]() Сравнивая координаты векторов, мы видим, что они - непропорциональные числа, делаем вывод, что векторы - не коллинеарные. 2) Проверим компланарность векторов. Предположим, что вектор
Сравнивая координаты векторов, мы видим, что они - непропорциональные числа, делаем вывод, что векторы - не коллинеарные. 2) Проверим компланарность векторов. Предположим, что вектор ![]() можно разложить по векторам
можно разложить по векторам ![]() .
. ![]() Если коэффициенты разложения х; у находятся однозначно, то векторы - компланарны и данные точки лежат в одной плоскости.
Если коэффициенты разложения х; у находятся однозначно, то векторы - компланарны и данные точки лежат в одной плоскости. ![]() . Составим и решим систему уравнени.
. Составим и решим систему уравнени.
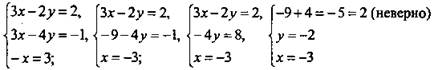
Вывод: векторы: ![]() - компланарны. Точки А; В; С; D не лежат в одной плоскости.
- компланарны. Точки А; В; С; D не лежат в одной плоскости.
II. Контролирующая самостоятельная работа
Цель работы: В течение 10-15 мин., в зависимости от уровня подготовленности класса, провести работу с целью проверки усвоения: а) нахождение координат вектора по заданным координатам точек - начала и конца вектора; б) нахождение координат вектора, выраженного через другие векторы, координаты которых заданы; в) нахождение коэффициента пропорциональности для коллинеарных векторов и параметрических переменных, входящих в заданные координаты векторов; г) использование понятия равных векторов; компланарных векторов при решении задач.
Контролирующая самостоятельная работа (см. приложение).
Решение контролирующей самостоятельной работы
I вариант |
II вариант |
Уровень А |
|
1. Дано: Найти: х; у; z. Решение:
|
1. Дано: Найти: х; у; z. Решение:
|
2. Дано: Найти: Решение:
|
2. Дано: Найти: Решение:
|
3. Дано: Найти: Решение:
|
3. Дано: Найти: Решение:
|
Уровень Б |
|
1. Дано: А(2; -1; 0), В(-3; 2; 1), С(1; 1; 4). Найти: D (х; у; z) | Решение:
|
1. Дано: А(2; -1; 0), В(-3; 2; 1), С(1; 1; 4). Найти: D (х; у; z) | Решение:
|
2. Дано: Найти: m; n. Решение:
|
2. Дано: Найти: m; n. Решение:
|
3. Дано: А(6; -1; 0), В(0; 3; -2), С(3; 1; -1). Доказать: А; В; С лежат на одной прямой. Какая из них лежит между двумя другими. Решение:
С лежит между А и В. .
|
3. Дано: А(0; 0; -1), В(5; -3; 1), С(-5; 3; -3). Доказать: А; В; С лежат на одной прямой. Какая из них лежит между двумя другими. Решение:
А лежит между С и В.
|
Уровень В |
|
1. Дано: А(2; -1; 0), В(-3; 2; 1), С(1; 1; 4), Найти: D (х; у; z) Решение:
D(11; -5; 2). |
1. Дано: А(2; -1; 0), В(-3; 2; 1), С(1; 1; 4), Найти: D (х; у; z) Решение:
D(0; -1/2; -1,5). |
2. Дано:
Найти: m; n. Решение:
|
2. Дано:
Найти: m; n. Решение:
|
3. Дано: A(1; 1; 1), В(-1; 0; -1), С(0; 2; 2), D(2; 0; 0). Установить: А; В; С; D лежат ли в одной плоскости. Решение:
1) 2) Проверим компланарность векторов. Предположим, что вектор
(2): 0 + 1 = 1; 1 = 1 (верно) векторы |
3. Дано: А(1; 0; -1), В(-2; -1; 0), С(0; -2; -1), D(1; 5; 0). Установить: А; В; С; D лежат ли в одной плоскости. Решение:
1)
2) Проверим компланарность векторов. Предположим, что вектор
-5 = -5 (верно) векторы |
III. Объяснение нового материала
1. Координаты середины отрезка
Пусть А(х2; у2; z2), В(х2; у2; z2) (рис. 1). Найдем координаты середины отрезка АВ - точки С(х; у z).
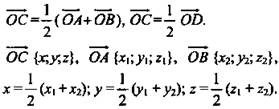
Итак, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
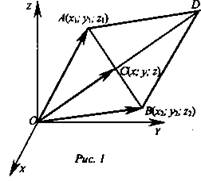
2. Вычисление длины вектора по его координатам (рис. 2).
![]()
Найдем длину вектора ![]() то есть
то есть ![]() Из прямоугольного параллелепипеда найдем длину диагонали ОА.
Из прямоугольного параллелепипеда найдем длину диагонали ОА. ![]()
![]()
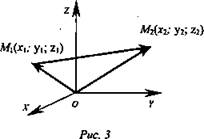
3. Расстояние между двумя точками (рис. 3).
Пусть M1(x1; y1; z1), M2(x2; y2; z2), ![]()
![]()
![]() Подставляя в формулу (1) получаем
Подставляя в формулу (1) получаем ![]()
![]()
Это доказательство ученики проводят в тетрадях самостоятельно.
IV. Закрепление нового материала
Отработка полученных знаний, умений и навыков.
К доске вызываются 2 ученика, которые решают № 424 а), 426 а).
Задача № 424 а).
Дано: А(0; 3; -4), В(-2; 2; 0), М- середина АВ.
Найти: М(х; у; z).
Решение: ![]()
![]()
(Ответ: М(-1; 2,5; -2).)
Задача № 426 а).
Дано: А(-1; 0; 2), B(1; -2; 3).
Найти: ![]()
Решение:
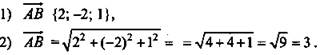
(Ответ: ![]() )
)
V. Демонстрация слайда
Точка пересечения медиан треугольника.
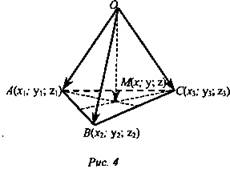
М - точка пересечения медиан треугольника ABC, О - начало координат (рис. 4.) A(x1; y1; z1); B(x2; y2; z2); C(x3;y3;z3); M(x; y; z).
![]()
![]()
![]()
VI. Подведение итогов
Сегодня мы на уроке проверили усвоение правил нахождения координат вектора, коэффициента пропорциональности для коллинеарных векторов. Вывели формулы для вычисления координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками. Отрабатывали умения и навыки решения стереометрических задач координатновекторным методом.
Домашнее задание
Уровень А: № 424 б); в); 425 а); 426.
Уровень Б: + № 429.
Творческое задание: составить карточки-задания номеров, аналогичных номерам в самостоятельной работе и задачам № 424—426.
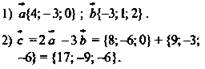
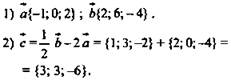


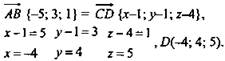
 D(-2; 0; -3).
D(-2; 0; -3).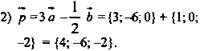
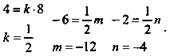

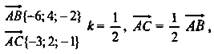
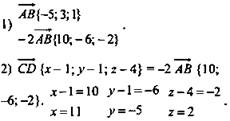
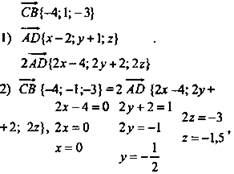
 - коллинеарные.
- коллинеарные.