Поурочные разработки по Геометрии 11 класс
Повторение. Двугранный угол. Перпендикулярность плоскостей - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цели урока:
- организовать повторение основных теоретических фактов по заданным темам;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация опорных знаний учащихся
Теоретический опрос.
1. Определение перпендикулярности прямой и плоскости.
2. Признак перпендикулярности прямой и плоскости.
3. Двугранный угол.
4. Определение перпендикулярности плоскостей.
5. Признак перпендикулярности двух плоскостей.
6. Свойства прямоугольного параллелепипеда.
Проверка домашнего задания.
Задача № 143.
Расстояние от точки М до каждой из вершин правильного ΔАВС равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.
Дано: ΔАВС - правильный, М ∈ ABC АВ = 6 см, АМ = ВМ = СМ = 4 см (рис. 1).
Найти: ρ(М, пл. ABC).
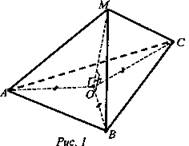
Решение: Проводим МО ⊥ пл. ABC, соединим точку О с А, В, С. Равные наклонные имеют равные проекции, поэтому АО = ОВ = ОС = R, где R - радиус окружности, описанной около ΔАВС. По теореме синусов ![]() Из прямоугольного ΔАОМ: ρ(М, пл. ABC):
Из прямоугольного ΔАОМ: ρ(М, пл. ABC): ![]()
![]() (Ответ: 2 см.)
(Ответ: 2 см.)
Задача № 149. Отрезок AD перпендикулярен к плоскости равнобедренного ΔАВС. Известно, что АВ = АС = 5 см, ВС = 6 см, AD = 12 см. Найдите расстояние от концов отрезка AD до прямой ВС.
Дано: ΔАВС, АВ = АС = 5 см, ВС = 6 см, AD ⊥ пл. ABC, AD = 12 см (рис. 2).
Найти: S (D; ВС); S (А, ВС).
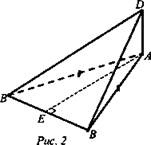
Решение:
1) Проведем AE ⊥ BC, в равнобедренном ΔАВС АЕ - высота и медиана, ВЕ = ЕС = 3 см. По теореме Пифагора из ΔСЕА: ![]()
![]()
2) Соединим точки D, Е. ВС ⊥ АЕ - по построению; ВС ⊥ DA - по условию ⇒ по теореме о трех перпендикулярах BC ⊥ DE.
3) ΔDEA - прямоугольный, по теореме Пифагора ![]()
![]() (Ответ: 4 см, 4√10 см.)
(Ответ: 4 см, 4√10 см.)
Решение задач по готовым чертежам
1. Дано: KLMN - тетраэдр, все ребра его равны. Точка О - середина ребра MN (рис. 3).
Доказать: ∠KOL - линейный угол двугранного угла LNMK.
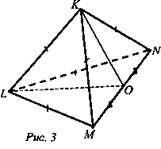
Доказательство:
1) ΔKMN - равносторонний, КО - медиана, следовательно, KO ⊥ MN.
2) ΔLMN - равносторонний, LO - медиана, следовательно LO ⊥ MN.
3) По определению линейного угла, ∠KOL - линейный угол двугранного угла LNMK.
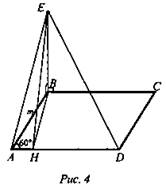
2. Дано: ABCD - ромб, ∠A = 60°, АВ = m, BE ⊥ ABC, ![]() (рис. 4).
(рис. 4).
Найти: угол между плоскостями ADE и ABC.
Решение:
1) ВН - высота ромба ABCD, EH ⊥ AD (по теореме о трех перпендикулярах). Значит, ∠EHB - линейный угол двугранного угла EADB.
2) ΔВНА: ![]()
3) ΔЕВН: ![]() (Ответ: 45°.)
(Ответ: 45°.)
III. Решение задач
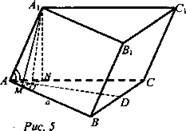
№ 1. Дано: АВСА1В1С1 - наклонная призма, ABC — правильный треугольник, ![]()
![]() (рис. 5).
(рис. 5).
а) Докажите: грань ВВ1С1С - прямоугольник.
б) Вычислите площадь грани АА1В1В.
в) Вычислите площадь полной поверхности.
г) Составить план вычисления объема призмы.
Решение:
а) Построим из вершины А1 перпендикуляр к плоскости А ВС - A1O и перпендикуляры к прямым АВ и АС - А1М и A1N соответственно. Тогда ОМ - проекция А1М, ON - проекция A1N на плоскость ABC. По теореме о трех перпендикулярах ОМ ⊥ AВ, ON ⊥ AC. ΔА1МА = ΔА1NA (по гипотенузе и острому углу). Значит, ON = ОМ, т. е. точка О - равноудалена от сторон АВ и АС, и значит лежит на биссектрисе AD. Так как ΔАВС - равносторонний, то AD ⊥ BC, АО - проекция АА1, на плоскость ABC. По теореме о трех перпендикулярах AA1 ⊥ BC, а значит, ВВ1 ⊥ BС, СС1 ⊥ BС, т. е. ВВ1С1С - прямоугольник.
б) АА1В1В - параллелограмм. ![]()
в) ![]() ВВ1С1С - прямоугольник,
ВВ1С1С - прямоугольник, ![]()
![]() значит,
значит, ![]()
![]()
г) Из ΔАМА1 найдем АM и A1M; из ΔАОМ найдем ОМ; из ΔА1ОМ найдем A1O. Зная высоту A1O n Sосн. найдем объем.
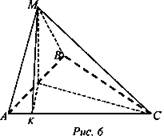
№ 2. Основанием пирамиды МАВС является равносторонний ΔАВС со стороной а. Грань МАВ - равнобедренный треугольник, плоскость которого перпендикулярна плоскости основания пирамиды. ![]() (рис. 6).
(рис. 6).
Найти: углы наклона боковых граней пирамиды к ее основанию.
Решение:
1) Высоты ΔАМВ и ΔАВС, проведенные из М и С, являются медианами, поэтому пересекаются в точке D. ∠MDC = 90° - линейный угол данного двугранного угла МАВС.
2) Проведем DK ⊥ AC, то AC ⊥ MK (по теореме о трех перпендикулярах). ∠MKD - линейный угол двугранного угла МАВС.
3) Из ΔMAD: ![]() Из ΔAKD:
Из ΔAKD: ![]() Из ΔMKD:
Из ΔMKD: ![]() (Ответ: 90°, 45°, 45°.)
(Ответ: 90°, 45°, 45°.)
№ 3. Через образующую цилиндра проведены два сечения. Одно из них является осевым сечением цилиндра, его площадь равна 48 см2. Угол между плоскостями сечений 60°. Вычислить площадь второго сечения (рис. 7).
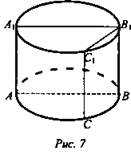
Решение: ![]() ΔABC - прямоугольный, т. к. АВ - диаметр; ∠ABC = 60° (по условию). Значит,
ΔABC - прямоугольный, т. к. АВ - диаметр; ∠ABC = 60° (по условию). Значит, ![]()
![]() (Ответ: 24 см2.)
(Ответ: 24 см2.)
IV. Подведение итогов
- Назовите необходимые условия перпендикулярности двух плоскостей.
Домашнее задание
Повторить гл. И, № 212, 216.