Поурочные разработки по Геометрии 11 класс
Объем прямоугольного параллелепипеда - Объем прямоугольного параллелепипеда - ОБЪЕМЫ ТЕЛ
Цели урока:
- закрепление знаний, умений и навыков учащихся по изученной теме, устранение пробелов в знаниях.
- совершенствование навыков решения задач на применение теорем об объеме прямоугольного параллелепипеда и следствия 1 и 2.
Ход урока
I. Организационный момент
II. Проверка домашнего задания (самопроверка)
На доске решения задач.
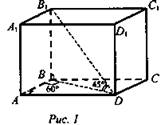
Задача № 656. Дано: ABCDA1B1C1D1 ∠B1DB = 45°. ∠A1B1BD = 60° - двугранный угол. BD = 12 см (рис. 1).
Найти: V.
Решение.
1. В прямоугольном параллелепипеде грани - прямоугольники. АС = BD = 12 см. A1B1 || АВ; АВ ⊥ B1B; BD ⊥ BB1; ∠ABD = 60° - линейный угол двугранного угла A1B1BD.
2. ΔB1BD : B1B = BD = 12 см. ΔABD: ![]()
![]() (Ответ: 432√3.)
(Ответ: 432√3.)
Задача № 658. Дано: АВСА1В1С1 - прямая призма. ∠BAC = 90°, ВС = 37 см, AB = 35 см, АА1 = 1,1 дм = 11 см (рис. 2).
Найти: V.
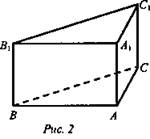
Решение:
1. ![]() (по следствию 2);
(по следствию 2); ![]()
![]()
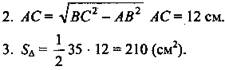
4. ![]() (можно 2,31 дм3). (Ответ: 2310 см3.)
(можно 2,31 дм3). (Ответ: 2310 см3.)
III. Устная работа по готовым чертежа.
Найти: V.
1) рис. 3
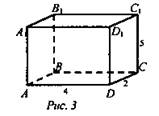
![]()
2) рис. 4

![]()
3) Письменно (по готовому чертежу.
Дано: B1D = d (рис. 5).
Найти: V.

Решение:
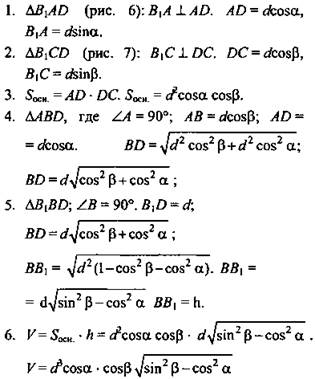
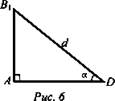
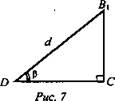
(Ответ: ![]() .)
.)
IV. Самостоятельная работа (контролирующего характера на 12 мин.
Вариант I
1. Измерения прямоугольного параллелепипеда равны 2,5 см, 5 см, 5 см. Найти ребро куба, объем которого в два раза больше объема данного параллелепипеда.
![]()
2. Найти объем прямой призмы АВСА1В1С1, если ∠ACB = 90°; ∠BAC = 30°; АВ = а; СВ = ВВ1 (рис. 8).
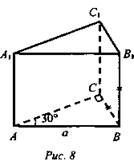
Решение: ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Вариант II
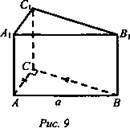
1. Измерения прямоугольного параллелепипеда равны 2 см, 6 см, 6 см. Найти ребро куба, объем которого в три раза больше объема данного параллелепипеда (рис. 9).
![]()
![]()
2. Найти объем прямой призмы АВСА1В1С1, если ∠ACB = 90°, АВ = ВВ1 = а; АС = СВ. Vпр. = Sосн. · h. ΔАСВ: ∠C = 90°, АС = СВ, значит ∠A = 45° = ∠B. АС = АВ · cos45°. ![]() (Ответ: a3/4.)
(Ответ: a3/4.)
V. Подведение итогов
- Как определить объем прямоугольного параллелепипеда?
Домашнее задание
№ 657. Подготовить I В. - п. 65; II В. - п. 66.