Поурочные разработки по Геометрии 11 класс
Понятие объема. Объем прямоугольного параллелепипеда - Объем прямоугольного параллелепипеда - ОБЪЕМЫ ТЕЛ
Цели урока:
- ввести понятие объема тела;
- рассмотреть свойства объемов, теорему об объеме прямоугольного параллелепипеда.
Ход урока
I. Организационный момент
II. Объяснение нового материала
1. Объем - одна из основных величин, связанных с геометрическими телами. Задача вычисления объемов простейших тел, идущая от практических потребностей, была одним из стимулов развития геометрии. Математика Древнего Востока (Вавилония, Египет) располагала рядом правил для вычисления объема тел, с которыми чаще всего приходилось встречаться на практике (призматические брусья; пирамиды полные и усеченные, цилиндры). Среди формул объема были и неточные, дававшие не слишком заметную процентную ошибку лишь в пределах употребительных линейных размеров тела. Но в «началах» Евклида и в сочинениях Архимеда имеются только точные правила для вычисления объемов многоугольников и некоторых круглых тел (цилиндра, конуса, шара и их частей).
Чтобы найти объем сначала выбирают единицу измерения. В Древнем Риме, например, одной из единиц объема служила амфора (около 25,5 л). Нефть во всем мире принято сейчас измерять в англо-американских единицах - баррелях, т. е. бочках емкостью 159 л. В России распространенная в быту мера объема - ведро.
2. Ну а в геометрии за единицу объема принимают объем куба с ребром единичной длины. Подчеркнем, что объем куба полностью определяется длиной ребра.
1 см3 - это куб с ребром 1 см.
1 м3 - это куб с ребром 1 м и т.д.
Объем - это положительная величина.
Свойства объемов:
1. Равные тела имеют равные объемы (рис. 159 а), б) в учебнике).
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 160 в учебнике).
3. Если одно тело содержит другое, то объем первого тела не меньше объема второго.
Следствие: объем куба с ребром 1/n равен 1/n3.
Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Дано: Р - прямоугольный параллелепипед, а, b, с - измерения, V - объем.
Доказать: V = а · b · с.
Доказательство:
1 случай.
а, b, с - конечные десятичные дроби, у которых число знаков после запятой не превосходит n (n ≥ 1).
а · 10n, b · 10n, с · 10n явл. целыми.
Разобьем ребра на равные части длины 1/10n. Р разобьем на a · b · c · 103n равных кубов с ребром 1/10n; ![]() то
то ![]() Итак V = abc. .
Итак V = abc. .
2 случай (необязательное).
Когда одно из измерений а, b, с - представляет собой бесконечную десятичную дробь.
Рассмотрим конечные десятичные дроби аn, bn, сn, которые получаются из чисел а, b, с если отбросить в каждом из них все цифры после запятой, начиная с (n + 1)-й.

Так как параллелепипед Р содержит в себе параллелепипед P’n, а сам содержится в параллелепипеде P’n, то объем V параллелепипеда Р заключен между ![]() т. е.
т. е. ![]() тогда
тогда ![]() значит, число а'nb'nс'n будет сколь угодно мало отличаться от числа аnbnсn. В силу неравенств (1) и (2) следует, что число V сколь угодно мало отличается от числа abc. Значит, они равны: V = abc, что и требовалось доказать.
значит, число а'nb'nс'n будет сколь угодно мало отличаться от числа аnbnсn. В силу неравенств (1) и (2) следует, что число V сколь угодно мало отличается от числа abc. Значит, они равны: V = abc, что и требовалось доказать.
Следствие 1.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
![]()
III. Закрепление изученного материал.
Задача № 647 б).
Тело R состоит из тел Р и Q, имеющих соответственно объемы V1 V2. Выразить объем V тела R через V1 V2 если б) тела Р и Q имеют общую часть, объем которой равен ![]()
Решение: ![]()
Задача № 648 а), б).
Найти объем прямоугольного параллелепипеда, стороны основания которого равны а и b, а высота равна h, если: а = 11, b = 12, h = 15;
б) ![]()
I B (а): ![]()
II В (б): ![]()
Задача № 649 б).
Дано: ABCDA1B1C1D1 - куб, АС1 = 3√2 (рис. 1).
Найти: V.
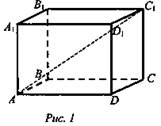
Решение: Пусть ребро куба равно а, тогда ![]()
![]() (Ответ: 6√6 см3.)
(Ответ: 6√6 см3.)
Задача № 651.
Кирпич имеет форму прямоугольного параллелепипеда с измерениями 25 см, 12 см и 6,5 см. Плотность кирпича равна 1,8 г/см3. Найти его массу.
Решение: ![]()
![]() (Ответ: 3,51 кг.)
(Ответ: 3,51 кг.)
IV. Подведение итогов
Домашнее задание
П. 63-64 (до следствия 2). № 648 в), г), 649 в), 652.