Разные задачи на многогранники, цилиндр, конус и шар - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- ввести понятие вписанного шара (сфера) в многогранник, описанного шара (сферы) около многогранника, выяснить условия их существования;

- научить учащихся применять введенные понятия при решении задач на комбинацию: сферы и пирамиды; цилиндра и призмы.

Ход урока

I. Организационный момент

Постановка целей и задач урока.

II. Актуализация знаний

Новые понятия, определения вписанного (описанного) шара (сферы) можно вводить по аналогии с вписанным (описанным) многоугольником.

- Какой многоугольник называется вписанным в окружность?

- Всякий ли треугольник можно вписать в окружность?

- Где находится центр окружности, описанной около треугольника?

- Где будет находится эта точка (центр окружности) в остроугольном, прямоугольном, тупоугольном треугольнике? (Внутри треугольника, на середине гипотенузы, вне треугольника).

- Какие мы знаки формулы для нахождения R?

- Всякий ли четырехугольник можно вписать в окружность? (Нет).

- Каким свойством обладает четырехугольник, вписанный в окружность? (Сумма противолежащих углов равна 180°).

- Какой многоугольник называется описанным около окружности?

- Где находится центр окружности вписанной в треугольник?

- Каким свойством обладает четырехугольник, описанный около окружности? (Сумма длин противолежащих сторон равна).

III. Изучение нового материала

Рассмотрим последовательность изложения теории по заданной теме.

1. Положение общих терминов, которые встречаются в задачах: многогранник, описанный около сферы; сфера, вписанная в многогранник; многогранник вписанный в сферу; сфера описанная около многогранника. (См. учебник с. 138).

Рассмотрение рисунков № 157 (а, б) и 158 а, б) на с. 139 учебника.

2. Теория на комбинацию сферы и пирамиды,

а) Шар вписанный в пирамиду.

- В любую треугольную пирамиду можно вписать шар.

- В пирамиду, у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать шар.

- В любую правильную пирамиду можно вписать шар.

- Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.

- Центр (сферы) шара, вписанного в правильную пирамиду, лежит на высоте этой пирамиды.

Решить задачу № 633. Возьмем треугольную пирамиду.

Дано: SABC - правильная пирамида; SD - высота пирамиды, сфера (О; R) (рис. 1).

Доказать: О ∈ SD.

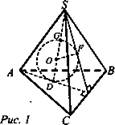
Доказательство: Проведем АЕ ⊥ ВС, отрезок SE. По теореме о трех перпендикулярах SE ⊥ СВ. Впишем в ΔSDE полуокружность DFG, центр О которой лежит на катете SD, а дуга касается сторон DE и SE. ΔSED вместе с полуокружностью DFG будем поворачивать вокруг SD. Тогда катет DE опишет окружность, вписанную в ΔАВС, поэтому гипотенуза SE при вращении остается внутри пирамиды, за исключением трех положений, когда SE будет совпадать с высотой боковых граней. Вывод: сфера, образованная вращением полуокружности DFG, будет иметь единственную общую точку с каждой из боковых граней. Эта сфера касается и основания пирамиды в точке D. Тогда центр вписанной в пирамиду SABC сферы (О; R) лежит на высоте SD.

б) Описанный шар около пирамиды.

- Около любой треугольной пирамиды можно описать шар.

- Если около основания пирамиды можно описать окружность, то около пирамиды можно описать шар.

- Около любой правильной пирамиды можно описать шар.

- Центр шара, описанного около пирамиды, лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.

Решить задачу № 639, в).

Дано: сфера (О; R), DABC - правильный тетраэдр. DH - высота тетраэдра; R - радиус сферы (рис. 2).

Найти: S полной поверхности тетраэдра.

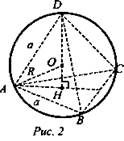
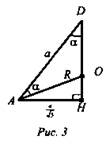
Решение: Примем ребро тетраэдра равно а. Центр О описанной сферы лежит на высоте DH, точка H - центр ΔАВС, поэтому Из прямоугольного ΔADH (рис. 3): где α = ∠ADH. Из ΔAOD по теореме косинусов: Площадь одной грани тетраэдра равна все грани - равносторонние треугольники, поэтому (Ответ: )

IV. Решение задач

Задача № 629. Дано: цилиндр, OO1 - ось цилиндра; АВСА1В1С1 - вписанная призма, OO1 ∈ (АА1В1В) (рис. 4).

Доказать: ∠((ACC1), (BСС1)) = 90°.

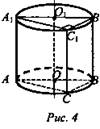
Доказательство: В окружности основания АВ диаметр, ∠ACB - вписанный, опирающийся на диаметр, значит, ∠ACB = 90°. ВС ⊥ CC1, образующая СС1 перпендикулярна основанию; ВС ⊥ (ACC1). По признаку перпендикулярности двух плоскостей (п. 23) плоскость АА1С1С перпендикулярна плоскости ВСС1В1.

Задача № 363. Дано: FDCDA1B1C1D1 - правильная усеченная пирамида, OO1 - высота, KN - апофема; сфера (S; R) (рис. 5).

Доказать:

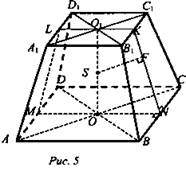
Доказательство: Боковые грани - равнобедренные трапеции; высоты этих трапеций называются апофемами. В правильной усеченной пирамиде центр вписанной сферы находится в середине OO1, где О и O1 - центры оснований. Это утверждение вытекает из вывода задачи № 633, центр сферы, вписанной в правильную пирамиду, лежит на высоте.

Из планиметрии: в описанном четырехугольнике суммы противоположных сторон равны (рис. 6).

в основаниях квадраты, LK = A1B1 = В1С1 и MN = АВ = ВС.

Доказано.

V. Подведение итогов

Цель, урока достигнута. Применили знания, полученные при изучении темы «Вписанные и описанные сферы в многогранник» при решении задач.

Домашнее задание

№ 635, 637. Стр. 138-139.

Доп. II уровень. Вычислите поверхность шара, вписанного в треугольную пирамиду, все ребра которой равны а.

Решение: Проведем плоскость через SO и SD. Радиус круга в полученном сечении равен радиусу шара. Так как все ребра пирамиды равны а, то Из ΔSOD ∠O = 90°, Обозначим радиус шара через R, тогда SO1 = SO - R. В ΔSKO1 имеем или т. е. (Ответ: )