Прямоугольная система координат в пространстве - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- ввести понятие прямоугольной системы координат в пространстве;

- выработать умение строить точку по заданным координатам и находить координаты точки, изображенной в заданной системе координат.

Ход урока

I. Организационный момент

Сообщить тему урока и сформулировать цели.

II. Устная работа

1. Даны точки А(-1; 7) и В(7; 1).

а) Найдите координаты середины отрезка АВ [С(3; 4)].

б) Найдите длину отрезка АВ (|АВ| = 10).

2. Запишите координаты вектора

3. Среди векторов укажите пару коллинеарных векторов

4. Е(-2; 3), F(1; 2). Найдите координаты вектора

5. Найдите расстояние между точками А(а; о) и В(b; о). (d = |b - а|).

III. Изучение нового материала

1. Вопрос 1. Сколькими координатами может быть задана точка на прямой? (Одной.)

Вопрос 2. Сколькими координатами может быть задана точка в координатной плоскости? (Двумя.)

Тогда в пространстве, по-видимому, точка может быть задана тремя координатами.

2. Объяснить, как задается прямоугольная система координат в пространстве и ее построение на плоскости. Прямоугольная система координат в пространстве задана, если выбрана точка - начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление (оно обозначается стрелкой) и задана единица измерения отрезков.

Желательно склеить из плотной бумаги разлинованной на клетки, модель системы координат в пространстве с разноцветными плоскостями.

3. Используя рисунок 114 учебника, обратить внимание на обозначения и названия осей координат в пространстве, сопоставить эти обозначения с соответствующими обозначениями осей координат на плоскости, известными из курса алгебры и геометрии VII-IX классов.

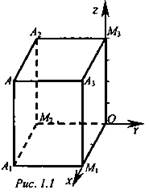
4. Подчеркнуть, что в прямоугольной системе координат каждой точке М пространства соответствует тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости. Для определения координат точки М в пространстве через эту точку проводят три плоскости, перпендикулярные к осям координат. Затем, использя точки М1, М2, M3 пересечения этих плоскостей с осями координат, находят координаты точки М (рис. 115 учебника).

5. Обратить внимание на нахождение координат точек, лежащих в координатных плоскостях или на осях координат.

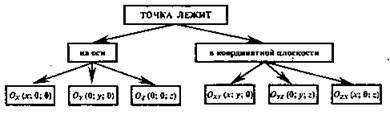
IV. Закрепление изучаемого материала

Для закрепления навыков нахождения координат точек и построения точек по заданным координатам можно использовать задачи № 400-402. При их решении целесообразно в некоторых случаях построить точки на рисунке по заданным координатам, хотя на поставленные вопросы можно ответить устно без рисунков.

Задача № 400 а), г) (Устно).

Задача № 401 а).

Дано: точка А(2; -3; 5).

Найти: координаты проекций этой точки на координатные плоскости.

Решение: Воспользуемся нашей таблицей. Так как нам необходимо узнать координаты проекций на координатные плоскости, рассмотрим точку А1 - проекцию на плоскость Оху. Значит А1 - лежит в плоскости Оху и ее координаты А(2; -3; 0). А2 - проекция точки А на плоскость xOz и ее координаты (2; 0; 5). А3 - проекция точки А на плоскость yOz и ее координаты (0; -3; 5) (рисунок 1.1 можно не рисовать).

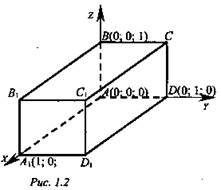
Задача № 402.

Дано: координаты четырех вершин куба ABCDA1B1C1D1. А(0; 0; 0), B(0; 0; 1), D(0; 1; 0), A1(1; 0; 0).

Найти: координаты остальных вершин.

Решение: Изобразим на рисунке систему координат Axyz и отметим точки В1, D1, А1. Проведем через эти точки плоскости, перпендикулярные осям координат. В результате получится куб ABCDA1B1C1D1 (рис 1.2). Видно, что вершины С, В1, С1, D1 имеют следующие координаты: С(0; 1; 1), B1(1; 0; 1), С1(1; 1; 1), D1(1; 1; 0).

V. Итог урока

- Итак, мы рассмотрели прямоугольную систему координат и научились строить точки по заданным координатам и находить координаты точки, изображенной в системе координат.

Домашнее задание

1) П. 42, № 400 (б, д), 401 (для точки В), повторить пп. 34-41.

2) П. 42, № 400 (б, в, д, е), № 401, пп. 34-41.