Решение задач по теме «Движения» - Движения - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- закрепление теоретических знаний по изучаемой теме;

- совершенствование навыков решения задач.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

Фронтальная работа с классом: теоретический опрос по вопросам:

1. Что называется движением пространства?

2. Приведите примеры движений.

3. Какое отображение пространства на себя называется центральной симметрией?

4. Какое отображение пространства на себя называется осевой симметрией?

5. Что называется зеркальной симметрией?

6. Какое отображение пространства на себя называется параллельным переносом?

7. Какие координаты имеет точка А, если при центральной симметрии с центром А точка, В(1; 0; 2) переходит в точку С(2; -1; 4). (Ответ: А(1,5; -0,5; 3).)

8. Как расположена плоскость по отношению к осям координат Ох и Oz, если при зеркальной симметрии относительно этой плоскости точка М(2; 2; 3) переходит в точку М1(2; -2; 3). (Ответ: Плоскость, относительно которой рассматривается зеркальная симметрия при которой точка М(2; 2; 3) переходит в точку М1(2; -2; 3), параллельна осям Ох и Oz.)

9. В какую перчатку (правую или левую) переходит правая перчатка при зеркальной симметрии? (Ответ: в левую), осевой симметрии? (Ответ: левую), центральной симметрии? (Ответ: правую).

В то время, когда идет фронтальная работа с классом, ученик решает задачу № 480 (а) у доски (проверка домашнего задания).

Задача № 480 а).

Докажите, что при центральной симметрии плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.

Решение:

1) Рассмотрим центральную симметрию пространства с центром О и произвольную плоскость а, не проходящую через точку О (рис. 1).

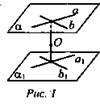
Пусть прямая а и b, пересекающиеся в точке А, лежат в плоскости а. При симметрии с центром О прямые а и b переходят соответственно в параллельные прямые а1 и b1 (см. № 479 а). При этом точка А переходит в некоторую точку А1, лежащую как на прямой а1, так и на прямой b1, а значит, прямые а1 и b1 пересекаются.

Пересекающиеся прямые определяют единственную плоскость, т. е. прямые а1 и b1 определяют плоскость а1. По признаку параллельности плоскостей а || а1.

2) Далее можно доказать, что при центральной симметрии с центром О плоскость а отображается на плоскость a1. Это можно доказать как в задаче № 479 1а), где было доказано, что прямая АВ отображается на прямую А1В1.

III. Решение зада.

Задача № 483 а).

При зеркальной симметрии относительно плоскости а плоскость β отображается в плоскость β1. Докажите, что если β || а1, то β1 || а.

Решение: Доказательство проведем методом от противного. Предположим, что β || а, но плоскости β1 и а пересекаются. Тогда они имеют общую точку М. Так как M ∈ а, то при данной зеркальной симметрии точка М отображается в себя. Отсюда следует, что точка М, которая принадлежит плоскости β1, лежит также в плоскости β. Но тогда плоскости а и β пересекаются. Полученное противоречие показывает, что наше предложение неверно, следовательно, β1 || а.

IV. Самостоятельная работа (см. приложение)

V. Подведение итогов

- Сегодня мы закрепили теоретические знания по теме «Движения» и отработали навыки использования их в процессе решения задач различного уровня сложности.

Домашнее задание

Решить задачи: № 480 (б), 483 (б) (подобные были рассмотрены на уроках).

Дополнительные задачи:

№ 519 (Указание: рассмотреть линейные углы двугранных углов, образованных плоскостями а и β, а и β1).

№ 520 (Указание: взять на плоскость а две пересекающиеся прямые и воспользоваться задачей № 484).

Центральная симметрия (рис. 2)

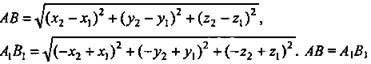
1. Докажите, что центральная симметрия есть движение.

2. Дан тетраэдр МАВС. Постройте фигуру, центрально-симметричную этому тетраэдру относительно точки О (рис. 3).

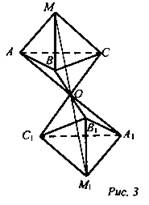
Слайд содержит теоретический материал справочного характера. По нему можно повторить теорию, провести опрос учащихся.

Этот слайд может быть использован при проверке результатов самостоятельной работы (I уровень).

Зеркальная симметрия

Плоскость а совпадает с плоскостью Оху (рис. 4).

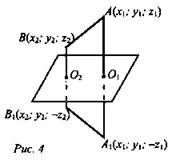
Точки O1 и О2 - середины отрезков АА1 и ВВ1.

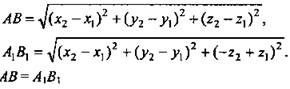
1. Докажите, что зеркальная симметрия есть движение (рис. 5).

2. Дан тетраэдр МАВС. Постройте фигуру, зеркально-симметричную этому тетраэдру относительно плоскости β.