Поурочные разработки по геометрии 10 класс
Контрольная работе № 3.1 по теме «Многогранники» - ПРАВИЛЬНЫЕ МНОГОГРАННИКИ - МНОГОГРАННИКИ
(см. приложение)
Цели урока:
1) проверить знания учащихся по теме «Многогранники», их умения применять полученные знания при решении конкретных задач;
2) выявить проблемы в знаниях учеников по указанной теме.
Решение контрольной работы
I уровень
Вариант I
№ 1. Дано: ABCA1B1C1 - прямая призма; ∠ACB = 90°; АС = 6 см; ВС = 8 см; АВВ1А1 - квадрат.
Найти: Sбок.
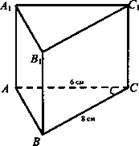
Решение:
1) ΔABC: АВ ![]() (по теореме Пифагора);
(по теореме Пифагора);
2) Наибольшая боковая грань – АВВ1А1, так как АВ - гипотенуза, тогда АВВ1А1 – квадрат АА1 = 10 см.
3) ![]() (Ответ: 240 см2.)
(Ответ: 240 см2.)
№ 2. Дано: SABCD - правильная четырехугольная пирамида; SA = 4 см, ∠SAD = 45°.
Найти a) SO; б) S6ок..
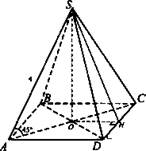
Решение:
1) ΔSАО - прямоугольный; ![]()
![]()
2) ΔAOD – прямоугольный; ![]()
![]()
3) ΔSOH - прямоугольный; ![]()
![]()
4) ![]() (Ответ:
(Ответ: ![]() )
)
№ 3. Дано: DABC - правильный тетраэдр; АВ = а.
Построить: (МКР) - сечение: М - середина AD, (МКР) || (DBC), МР || ВС, (КМР - искомое сечение).
Найти: SMKP.
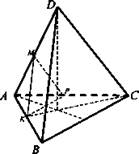
Построение: 1) MK || DB, MP || DC (по свойству секущей плоскости). Значит, (МКР) - искомое сечение.
2) МК - средняя линия в ΔABD ⇒ МК = a/2; КР, МР - средние линии в ΔABC и ΔADC соответственно, значит, КР = МР = 1/2а. ![]() (Ответ:
(Ответ: ![]() )
)
Вариант II
№ 1. Дано: АВСА1В1С1 - прямая призма; ΔАВС: ∠C = 90°; АВ = 13 см; ВС = 12 см.
Найти: Sбок.
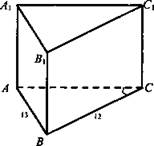
Решение:
1) ΔАВС - прямоугольный, ![]()
2) Грань АСС1А1 - наименьшая, так как АС - меньший катет, тогда АСС1А1 - квадрат, СС1 = 5 см.
3) ![]() (Ответ: Sбок. = 150 см2.)
(Ответ: Sбок. = 150 см2.)
№ 2. Дано: SABCD - правильная пирамида; SO= √6 см; ∠SAO = 60°.
Найти: a) SA; Sбок.
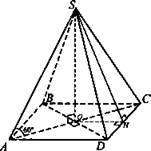
Решение:
1) ΔSAO - прямоугольный; ![]()
![]()
2) ![]()
3) ΔSOH - прямоугольный; ![]()
4) ![]() (Ответ:
(Ответ: ![]() )
)
№ 3. Дано: DABC - правильный тетраэдр; АВ = а.
Построить: сечение (МКР): К - середина AD; М - середина АВ; (КМР || ВС).
Найти: SMKP.

Решение:
1) КМ, МР, КР - средние линии ΔABD, ΔАВС, ΔADC соответственно, значит, КМ = МР = КР = 1/2а.
2) ![]() (Ответ:
(Ответ: ![]() )
)
II уровень
Вариант I
№ 1. Дано: ABCDA1B1C1D1 - прямой параллелепипед, ABCD - ромб, BD = 10 см; АС = 24 см; ∠B1DB = 45°.
Найти: Sполн.
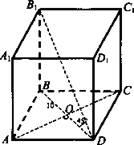
Решение:
1) ΔBB1D - прямоугольный. Меньшая диагональ параллелепипеда проектируется в меньшую диагональ основания ∠BDB1 = 45°, тогда ВВ1 = BD = 10 см;
2) ΔAOD - прямоугольный. ![]()
3) ![]()
![]() (Ответ: 760 см2.)
(Ответ: 760 см2.)
№ 2. Дано: SABC - пирамида; ΔАВС - правильный; SΔABC = 9√3 см2; (SBC) ⊥ (ABC), (SAC) ⊥ (ABC), ∠SHC = 30°.
Найти: a) SC, SA, SB; б) Sбок..
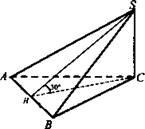
Решение:
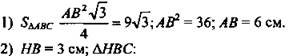
![]()

(Ответ: ![]() )
)
№ 3. Дано: ABCDA1B1C1D1 - куб: АВ = а.
Построить: сечение МВ1СК.
Найти: Sсeч.
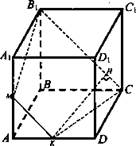
Решение:
1) По свойству секущей плоскости МК || В1С, тогда МВ1СК - искомое сечение.
2) МВ1СК - равнобокая трапеция; ΔАМК: ![]()
3) ΔВ1С1С: ![]()
4) ΔKDC - прямоугольный: 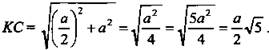
5) ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Вариант II
№ 1. Дано: ABCDA1B1C1D1 — прямой параллелепипед; ABCD - ромб: АС = 12 см - меньшая диагональ; BD1 = 16√2 см; ∠BB1D = 45°.
Найти. Sполн.
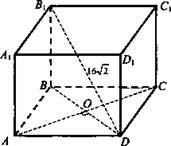
Решение:
1) ΔB1BD - прямоугольный: ![]()
![]() ВВ1 = BD = 16 см.
ВВ1 = BD = 16 см.
2) ΔAOD - прямоугольный: ![]()
3) ![]() (Ответ: Sполн. = 832 см2.)
(Ответ: Sполн. = 832 см2.)
№ 2. Дано: SABC - пирамида. ΔАВС - прямоугольный: АС = ВС; SC ⊥ (ABC); ∠SHC = 45°; АВ = 4√2 см.
Найти: a) SC, SA, SB; б) Sбок.
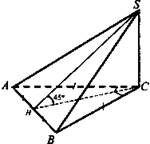
Решение:
1) ΔАВС - прямоугольный: ![]()
![]() АС = ВС = 4 см.
АС = ВС = 4 см.
2) ΔНВС- прямоугольный: ![]()
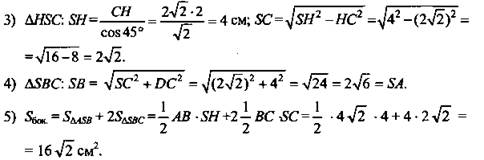
(Ответ: ![]() )
)
№ 3. Дано: ABCDA1B1C1D1 - куб: АВ = а.
Построить: сечение МВ1СК.
Найти: SМВ1СК.
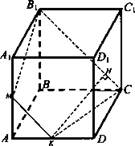
Решение:
1) По свойству секущей плоскости МК || В1С, тогда МВ1СК - искомое сечение.
2) МВ1 = КС, МВ1СК - равнобокая трапеция; 
3) ![]()
4) ΔKDC - прямоугольный. 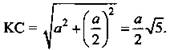
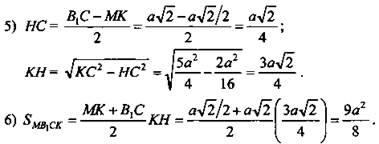
(Ответ: ![]() )
)
III уровень
Вариант I
№ 1. Дано: ABCA1B1C1 - прямоугольная призма; ΔABC: ∠C = 90°; AC = 20 см; ВС = 15 см; SС1H1HC - наименьшее сечение, проходящее через боковое ребро - квадрат.
Найти: Sполн.
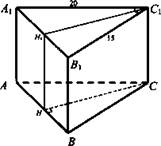
Решение:
1) ![]()
2) C1H1 – меньшая высота в ΔA1B1C1; ![]()
3) ![]()
![]() (Ответ: 1020 см2.)
(Ответ: 1020 см2.)
№ 2. Дано: SABCD - пирамида; ABCD - ромб; ∠A = α; АС = d; ∠SHO = β.
Найти: Sполн.
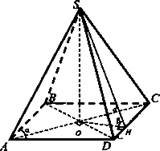
Решение.
1) ΔAOD - прямоугольный: ![]()
2) ΔOCH - прямоугольный: ![]() ΔOSH - прямоугольный:
ΔOSH - прямоугольный: ![]()
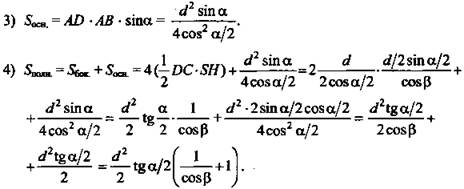
(Ответ : ![]() )
)
№ 3. Дано: ABCDA1B1C1D1 - куб; AB = а; M, К, P - середины ребер AA1, B1C1, CD) соответственно.
Построить: сечение, проходящее через точки М, К, Р.
Найти: Sсeч.
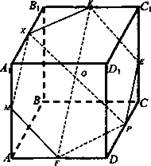
Решение: 1) МХ || PF (так как секущая плоскость пересекает противоположные грани по параллельным отрезкам). Значит, MF || КЕ, ХК || FP. Тогда MXKEPF - правильный шестиугольник: 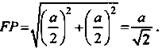
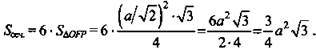 (Ответ:
(Ответ: ![]() )
)
Вариант II
№ 1. Дано: ABCDA1B1C1D1 - прямая призма. ΔАВС: АС = ВС = 13 см; АВ = 24 см. НН1С1С - квадрат - наименьшее сечение призмы, проходящее через боковое ребро.
Найти: Sполн.
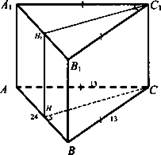
Решение:
1) ΔНВС - равнобедренный. ![]()
![]() HC = CC1 = 5 см.
HC = CC1 = 5 см.
2) ![]()
![]() (Ответ: Sполн. = 370 см2.)
(Ответ: Sполн. = 370 см2.)
№ 2. Дано: ABCD - ромб; SABCD - пирамида; ∠B = α; ∠SHO = β; SO = Н;
Найти: Sполн.
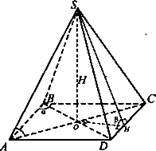
Решение: ![]()
1) ΔSOH - прямоугольный; ![]()
![]()
2) ΔHOD - прямоугольный; ![]()
![]()
3) ΔODC - прямоугольный; ![]()
4) ΔDOC - прямоугольный; ![]()
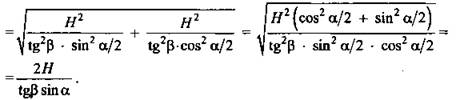
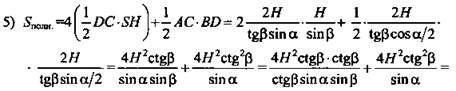
![]() (Ответ:
(Ответ: ![]() )
)
№ 3.
Аналогично № 3, вариант 1. (Ответ: ![]() )
)