Повторение (решение задач на теорему о 3-х перпендикулярах) - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цель урока:

- сформировать навык в решении задач с использованием теоремы о 3-х перпендикулярах.

Ход урока

I. Проверка домашнего задания (3 мин)

Вспомнить с учащимися формулировку теоремы о 3-х перпендикулярах. (Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.)

Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярна к ней, перпендикулярна и к ее проекции.

II. Работа в классе (15 мин)

Решить задачи № 158 и № 161 с объяснением у доски.

№ 158

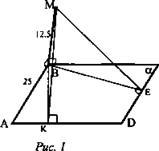
Через вершину В ромба ABCD проведена прямая ВМ перпендикулярно к его плоскости (рис. 1).

Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см; ∠BAD = 60°; ВМ = 12,5 см.

Решение:

1) Проведем ВК ⊥ AD. ВК - проекция наклонной МК на плоскость ромба; AD ⊥ ВК, то AD ⊥ МК (по теореме о 3-х перпендикулярах). Длина МК - расстояние от точки М до прямой AD. ME - расстояние от точки М до прямой DC.

2) Из треугольника АВК:

3) ΔМВК - прямоугольный (∠B = 90°), так как MB ⊥ (ABC);

4) ВК = BE (как высоты ромба); ΔМВК = ΔМВЕ (по двум катетам, как прямоугольные); ME = МК = 25 см.

5) Расстояние от точки М до прямых АВ и ВС равны длине перпендикуляра MB, то есть 12,5 см. (Ответ: 25 см; 25 см; 12,5 см; 12,5 см.)

№ 161

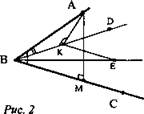
Луч ВА не лежит в плоскости неразвернутого ∠CBD. Докажите, что если ∠ABC = ∠ABD, причем ∠ABC < 90°, то проекцией луча ВА на плоскость CBD является биссектриса ∠CBD (рис. 2).

Решение:

1) Пусть АЕ ⊥ (CBD). В плоскости (ABC) проведем перпендикуляр AM к прямой ВС, а в плоскости (ABD) перпендикуляр АК к прямой BD.

Так как ∠ABC < 90°, то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ∠ABD < 90°, то точка К лежит на луче BD. Так как ВС ⊥ AM, то ВС ⊥ ЕМ (по теореме, обратной теореме о 3-х перпендикулярах).

Аналогично доказывается, что BD ⊥ ЕК.

2) ΔАВК и ΔАВМ равны по гипотенузе (АВ - общая) и острому углу (∠ABC = ∠ABD), то ВМ = ВК;

3) ΔВME и ΔВКЕ равны по гипотенузе (BE - общая) и катету (ВМ = ВК), то ЕМ = ЕК;

4) Точка Е равноудалена от сторон ∠CBD, значит, она лежит на биссектрисе этого угла, то есть луч BE - биссектриса ∠CBD.

III. Решение задач

У доски 2 ученика решают задачи № 199 и № 202, класс решает самостоятельно (20 мин). Затем учитель вместе с классом проверяет решение задач (с комментированием)

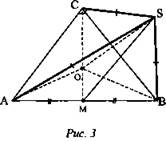
№ 199. Дано: SA = SB = SC, S ∉ (ABC), M - середина гипотенузы перпендикуляра к плоскости треугольника.

Доказать: SM ⊥ (ABC).

Решение:

1. ΔASB - равнобедренный; SM - медиана, то SM ⊥ АВ (это высота).

2. CM ∈ (SCM) проведем SO ⊥ СМ. Построим АО; ВО; СО.

3. AS = BS = CS - равные наклонные, то ОА = ОВ = ОС = R. R - радиус описанной окружности около ΔABC. SM ⊥ (ABC).

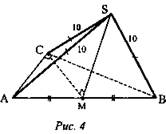
№ 202. Дано: ΔABC, АС ⊥ ВС, SA = SB = SC = 10 см; СМ = 5 см - медиана (рис. 4).

Найти: SM (расстояние от точки S до плоскости (ABC)).

Решение:

1) Прямая SM, М - середина гипотенузы АВ, перпендикулярна к плоскости (ABC) SM ⊥ (ABC).

2) (Ответ: 5√3 см.)

IV. Подведение итогов

При решении задач используется теорема о 3-х перпендикулярах.

Домашнее задание

П. 20, теорема о 3-х перпендикулярах.

Задачи: № 204, 206.

Урок 35. Повторение (решение задач на теорему о 3-х перпендикулярах)

Цель урока:

- сформировать навык в решении задач с использованием теоремы о 3-х перпендикулярах.

Ход урока

I. Проверка домашнего задания (3 мин)

Вспомнить с учащимися формулировку теоремы о 3-х перпендикулярах. (Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.)

Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярна к ней, перпендикулярна и к ее проекции.

II. Работа в классе (15 мин)

Решить задачи № 158 и № 161 с объяснением у доски.

№ 158

Через вершину В ромба ABCD проведена прямая ВМ перпендикулярно к его плоскости (рис. 1).

Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см; ∠BAD = 60°; ВМ = 12,5 см.

Решение:

1) Проведем ВК ⊥ AD. ВК - проекция наклонной МК на плоскость ромба; AD ⊥ ВК, то AD ⊥ МК (по теореме о 3-х перпендикулярах). Длина МК - расстояние от точки М до прямой AD. ME - расстояние от точки М до прямой DC.

2) Из треугольника АВК:

3) ΔМВК - прямоугольный (∠B = 90°), так как MB ⊥ (ABC);

4) ВК = BE (как высоты ромба); ΔМВК = ΔМВЕ (по двум катетам, как прямоугольные); ME = МК = 25 см.

5) Расстояние от точки М до прямых АВ и ВС равны длине перпендикуляра MB, то есть 12,5 см. (Ответ: 25 см; 25 см; 12,5 см; 12,5 см.)

№ 161

Луч ВА не лежит в плоскости неразвернутого ∠CBD. Докажите, что если ∠ABC = ∠ABD, причем ∠ABC < 90°, то проекцией луча ВА на плоскость CBD является биссектриса ∠CBD (рис. 2).

Решение:

1) Пусть АЕ ⊥ (CBD). В плоскости (ABC) проведем перпендикуляр AM к прямой ВС, а в плоскости (ABD) перпендикуляр АК к прямой BD.

Так как ∠ABC < 90°, то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ∠ABD < 90°, то точка К лежит на луче BD. Так как ВС ⊥ AM, то ВС ⊥ ЕМ (по теореме, обратной теореме о 3-х перпендикулярах).

Аналогично доказывается, что BD ⊥ ЕК.

2) ΔАВК и ΔАВМ равны по гипотенузе (АВ - общая) и острому углу (∠ABC = ∠ABD), то ВМ = ВК;

3) ΔВME и ΔВКЕ равны по гипотенузе (BE - общая) и катету (ВМ = ВК), то ЕМ = ЕК;

4) Точка Е равноудалена от сторон ∠CBD, значит, она лежит на биссектрисе этого угла, то есть луч BE - биссектриса ∠CBD.

III. Решение задач

У доски 2 ученика решают задачи № 199 и № 202, класс решает самостоятельно (20 мин). Затем учитель вместе с классом проверяет решение задач (с комментированием)

№ 199. Дано: SA = SB = SC, S ∉ (ABC), M - середина гипотенузы перпендикуляра к плоскости треугольника.

Доказать: SM ⊥ (ABC).

Решение:

1. ΔASB - равнобедренный; SM - медиана, то SM ⊥ АВ (это высота).

2. CM ∈ (SCM) проведем SO ⊥ СМ. Построим АО; ВО; СО.

3. AS = BS = CS - равные наклонные, то ОА = ОВ = ОС = R. R - радиус описанной окружности около ΔABC. SM ⊥ (ABC).

№ 202. Дано: ΔABC, АС ⊥ ВС, SA = SB = SC = 10 см; СМ = 5 см - медиана (рис. 4).

Найти: SM (расстояние от точки S до плоскости (ABC)).

Решение:

1) Прямая SM, М - середина гипотенузы АВ, перпендикулярна к плоскости (ABC) SM ⊥ (ABC).

2) (Ответ: 5√3 см.)

IV. Подведение итогов

При решении задач используется теорема о 3-х перпендикулярах.

Домашнее задание

П. 20, теорема о 3-х перпендикулярах.

Задачи: № 204, 206.