Демонстрационный вариант ГИА (факультативное занятие) - Государственная итоговая аттестация по алгебре (ГИА)

Цель: дать представление о структуре и сложности варианта, разобрать его и отметить его особенности.

Далее приведем варианты экзаменационной работы с решениями, по которым можно судить об уровне сложности заданий и их распределении по темам. В части 2 после номера задания в скобках указано число баллов за это задание. Рекомендуем вам самостоятельно выполнить варианты. В случае затруднений можно обратиться к разбору варианта.

Вариант № 1

Часть 1

1. Диаграмма иллюстрирует распределение учащихся школы между начальными, средними и старшими классами. Сколько процентов всех учащихся учится в 10-11 классах этой школы?

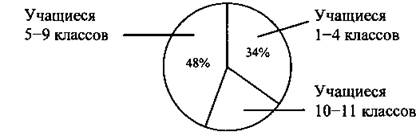
Ответ: ____________________

2. Найдите сумму, значение которой больше 1.

1) 0,45 + 1/3 .

2) 0,54 + 2/3

3) 2/9 + 1/3 + 1/6

4) 0,27 + 0,28 + 0,29

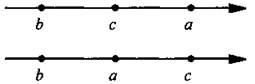
3. На координатной прямой точками изображены числа а и b. Определите, какое из чисел является наибольшим: 2а, 2b или а + b.

1) а + b .

2) 2а .

3) 2b

4) для ответа не хватает данных

4. Найдите значение выражения 1/9ху при

Ответ: ____________________

5. Принтер печатает одну страницу за 6 с. Сколько страниц можно распечатать на этом принтере за t мин?

1) 6t с .

2) 10t с

3) 0,1t с .

4) t/6 с

6. Упростите выражение .

Ответ: ____________________

7. Найдите значение выражения (27 · 3-4)2.

1) 1/9

2) 3

3) -9

4) -1/9

8. Упростите выражение

Ответ: ____________________

9. Решите уравнение

1) 1

2) 1,4

3) 5

4) 5,4

10. Какое из уравнений не имеет корней?

1) 2х - 3х + 1 = 0

2) 2х2 + 4х - 1 = 0

3) 3х2 + 4х + 1 = 0

4) 3х2 - 2х + 1 = 0

11. Для каждой системы уравнений укажите число ее решений. (Для ответа используйте графики; график уравнения х2 + у2 = 4 изображен на рисунке.)

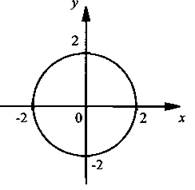
а) нет решений

б) одно решение

в) два решения

г) три решения

12. Какое из следующих чисел не является решением неравенства 9х – 3 > 10х - 2?

1) -4,9 .

2) -1,7

3) -1,1 .

4) -0,7

13. Сравните, если возможно, числа а и с при условии, что а > b и b ≤ с.

1) а > с .

2) а < с .

3) а ≤ с

4) сравнить невозможно

14. В зрительном зале 15 рядов. В первом ряду 10 мест, а в каждом следующем на одно место больше, чем в предыдущем. Сколько мест в зрительном зале?

1) 255 мест .

2) 165 мест .

3) 120 мест

4) 75 мест

15. На каком рисунке изображен график функции у = f(x), обладающей свойствами f(0) = 2 и функция возрастает на промежутке (-∞; 1]?

16. График показывает, как менялась цена бензина в течение месяца. Определите, на сколько процентов выросла его цена за месяц.

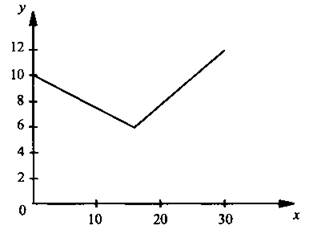
1) на 100%

2) на 60%

3) на 20%

4) на 2%

Часть 2

17. (2 балла.) Сократите дробь

18. (4 балла.) Постройте график функции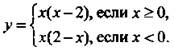

При каких значениях х функция принимает отрицательные значения?

19. (4 балла.) На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине ее можно сделать на 15 мин быстрее, чем на второй?

20. (6 баллов.) Найдите значение m, при котором точки А(3; 15), В(9; 5) и С(24; m) лежат на одной прямой.

21. (6 баллов.) При каких значениях k число 0 находится между корнями уравнения х2 - 4х + (2 - k)(2 + k) = 0?

Решение заданий работы

Часть 1

1. Число всех учащихся в школе примем за 100%, тогда число учащихся в 10-11 классах в соответствии с диаграммой: 100 – 48 – 34 = 18 (%).

Ответ: 18%.

2. Переведем обыкновенные дроби в десятичные и оценим приведенные суммы:

Видно, что только сумма второго ответа больше 1.

Ответ: 2.

3. Из приведенного рисунка видно, что a < 0 и b > 0.

Поэтому легко оценить числа: 2a < а < 0, a < a + b < b и 2b > b > 0. Итак, наибольшее число 2b.

Ответ: 3.

4. Подставим в выражение 1/9ху величины и получим:

Ответ: 2/3.

5. За 1 мин принтер распечатает 60/6 = 10 страниц. Поэтому за t мин принтер распечатает 10t страниц.

Ответ: 2.

6. Разложим знаменатель второй дроби на множители, приведем дроби к общему знаменателю и вычтем их. Получим:

Ответ:

7. Используя свойства действий со степенями, найдем значение выражения

Ответ: 1.

8. Во втором выражении вынесем множитель из-под корня и упростим выражение:

Ответ:

9. Все члены уравнения умножим на 6 и получим: 2х + 3(х - 1) = 24 ⇒ 2х + 3х - 3 = 24 ⇒ 5х = 27, откуда х = 5,4.

Ответ: 4.

10. Для приведенных квадратных уравнений найдем дискриминанты и получим:

1) 2х2 - 3х + 1 = 0, D = 9 – 4 · 2 · 1 = 1 > 0 (имеет 2 корня);

2) 2Х2 + 4х - 1 = 0, D = 16 – 4 · 2 · (-1) = 24 > 0 (имеет 2 корня);

3) 3х2 + 4х + 1 = 0, D = 16 – 4 · 3 · 1 = 4 > 0 (имеет 2 корня);

4) 3х2 - 2х + 1 = 0, D = 4 – 4 · 3 · 1 = -8 < 0 (не имеет корней).

Видно, что только уравнение 4 не имеет корней.

Ответ: 4.

11. Учтем, что второе уравнение системы задает параболу, направленную ветвями вверх. Рассмотрим три приведенные системы и получим:

1) парабола у = х2 выходит из начала координат и пересекает окружность х2 + у2 = 4 в двух точках. Поэтому такая система уравнений имеет два решения, т. е. 1 → в;

2) парабола у = х2 + 2 выходит из точки (0; 2) и имеет с окружностью х2 + у2 = 4 только эту одну общую точку. Поэтому такая система уравнений имеет одно решение, т. е. 2 → б;

3) парабола у = х2 + 3 выходит из точки (0; 3) и располагается выше окружности х2 + у2 = 4, т. е. не имеет с ней общих точек. Поэтому такая система уравнений не имеет решений, т. е. 3 → а.

Ответ: 1 → в; 2 → б; 3 → а.

12. Решим приведенное линейное неравенство 9х - 3 > 10х - 2 и получим: -3 + 2 > 10х - 9х, или -1 > х, т. е. х < -1. Видно, что число -0,7 (ответ 4) не входит в этот промежуток.

Ответ: 4.

13. Так как а > b и b ≤ с, то сравнить числа а и с невозможно. Например, на верхней шкале а > с, а на нижней, наоборот, а < с.

Ответ: 4.

14. Посчитаем число мест в рядах: 10, 11, 12, ... Видно, что эти числа образуют арифметическую прогрессию с первым членом а1 = 10 и разностью d = 1. Найдем сумму n = 15 первых членов прогрессии. Получаем: или (мест).

Ответ: 1.

15. Если функция y = f(x) возрастает на промежутке (-∞; 1], то эта функция имеет наибольшее значение при х = 1. При этом при х = 0 значение функции равно f(0) = 2. Этим условиям удовлетворяет только функция, график которой изображен на рис. 1.

Ответ: 1.

16. Из графика видно, что в начале месяца бензин стоил 10 руб., в конце месяца - 12 руб. Поэтому цена бензина увеличилась на 12 - 10 = 2 руб., что составляет 2/10 · 100 = 20% первоначальной цены бензина.

Ответ: 2.

Часть 2

17. (2 балла.) Разложим числитель и знаменатель дроби на множители и сократим ее. В числителе найдем корни квадратного трехчлена, в знаменателе используем группировку членов и вынесение общего множителя за скобки.

Получаем: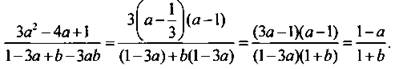

Ответ:

18. (4 балла.) Построим сначала график функции у = x(x - 2) - пунктирная парабола. Оставим тот участок кривой, для которого х ≥ 0. Теперь построим график функции у = х(2- х). Так как х(2 - х) = -х(х - 2), то при x < 0 надо отразить пунктирную часть параболы вниз. Поэтому графиком данной функции является сплошная кривая. Видно, что значения функции f(x) < 0 при х < 0 и 0 < х < 2.

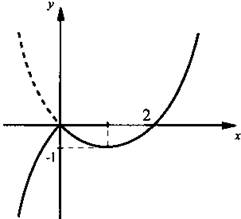
Ответ: f(x) < 0 при x < 0 и 0 < x < 2.

19. (4 балла.) Пусть на первой машине можно сделать копию пакета документов за t мин, тогда на второй - за t + 15 мин. Производительность машин соответственно (при этом весь объем работы принят за единицу). Так как при одновременной работе двух машин копию можно сделать за 10 мин, то получаем уравнение Корни этого уравнения t = 15 и t = -10 (не подходит). Итак, работа будет сделана на первой машине - за 15 мин, на второй - за 30 мин.

Ответ: на первой машине - за 15 мин, на второй - за 30 мин.

20. (6 баллов.) Пусть уравнение прямой у = kх + b. Так как ее график проходит через точки А(3; 15) и В(9; 5), то их координаты удовлетворяют уравнению прямой. Получаем систему линейных уравнений Вычтем из первого уравнения второе: 10 = -6k, откуда k = -5/3. Подставим это значение в первое уравнение: откуда b = 20. Итак, уравнение прямой у = -5/3x + 20. Эта прямая также проходит через точку С(24; m). Получаем m = -5/3 · 24 + 20 = -20.

Ответ: m = -20.

21. (6 баллов.) Так как число 0 находится между корнями уравнения х2 - 4х + (2 - k)(2 + k) = 0, то произведение корней уравнения (по формуле Виета) (2 - k)(2 + k) < 0. Решение этого неравенства: k < -2 и k > 2. Проверим, что уравнение имеет корни. Найдем D/4 = 4 - (2 - k)(2 + k) = 4 + (k - 2)(k + 2) = 4 + k2 - 4 = k2 ≥ 0, т. е. при всех значениях k данное уравнение имеет решения.

Ответ: при k < -2 и k > 2.

Вариант № 2

Часть 1

1. Одна из точек М, N, Р, Q, отмеченных на координатной прямой, соответствует числу Какая эта точка?

1) М

2) N

3) Р

4) Q

2. Что больше: 26% учащихся школы или 1/4 учащихся этой школы?

1) 26% учащихся

2) 1/4 учащихся

3) эти числа равны

4) данных для ответа недостаточно

3. Известно, что а - число нечетное. Какое из чисел также является нечетным?

1) 2а

2) а + 2

3) а - 1

4) а2 + 1

4. За n одинаковых тетрадей и m одинаковых блокнотов заплатили с руб. Тетрадь стоит а руб. Сколько стоит блокнот?

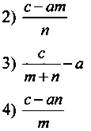
5. Для каждого выражения укажите множество значений переменной дг, при которых это выражение имеет смысл.

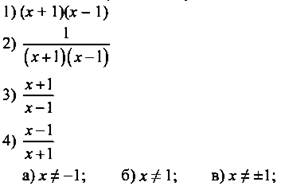г) х - любое число

6. Сократите дробь

Ответ: ___________________

7. Найдите значение выражения (с6с-3)-1 при c = 1/3.

1) 27

2) -27

3) 1/27

4) -1/27

8. Укажите выражение, тождественно равное произведению (х - 2)(х - 3).

1) (2 – х)(3 - х)

2) (2 - х)(х - 3)

3) (х - 2)(3 - х)

4) -(2 - х)(3 - х)

9. Решите уравнение х2 + 2х - 3 = 0.

Ответ: ___________________

10. Используя графики, решите систему уравнений

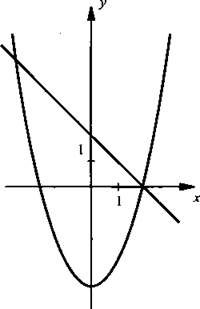
Ответ: ___________________

11. Бабушка прополола 15 грядок, после чего ее сменил внук, который прополол 14 грядок. Всего они работали 5 ч, причем внук за час пропалывал на 2 грядки больше, чем бабушка. Сколько грядок за 1 ч пропалывал каждый?

Пусть за 1 ч внук пропалывал х грядок. Какое уравнение соответствует условию задачи?

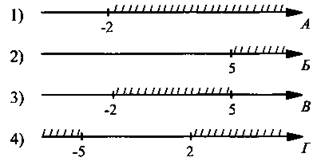
12. На каком рисунке изображено множество решений системы неравенств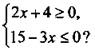

13. Известно, что 0 < а < 1. Сравните а и 1/a.

1) а > 1/a

2) а < 1/а

3) а = 1/а

4) сравнить невозможно

14. Разность d арифметической прогрессии равна 3. Какой формулой может быть задана эта арифметическая прогрессия?

1) аn = 5n - 3

2) аn = 5n + 3

3) аn = 3n - 5

4) аn = 5 - 3n

15. На рисунке изображен график функции у = f(x). Какое из следующих утверждений неверно?

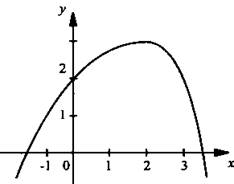
1) f(0) = 2

2) f(-2) < 0

3) функция возрастает на промежутке (-∞; 2]

4) нулями функции являются числа -1,5; 2; 3,5

16. На рисунке изображен график движения автомобиля из пункта А в пункт В и автобуса из пункта В в пункт А. На сколько километров в час скорость автомобиля больше скорости автобуса?

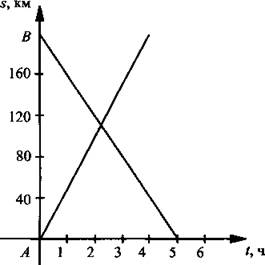
Ответ: ___________________

Часть 2

17. (2 балла.) Решите систему уравнений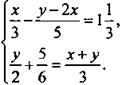

18. (4 балла.) Найдите область определения выражения

19. (4 балла.) Найдите сумму всех натуральных чисел, не превосходящих 200, которые делятся на 3.

20. (6 баллов.) Прямая 3х + 2у = с, где с - некоторое число, касается гиперболы у = 6/x в точке с положительными координатами. Найдите координаты точки касания.

21. (6 баллов.). Четыре бригады должны разгрузить вагон с продуктами. Вторая, третья и четвертая бригады вместе могут выполнить эту работу за 4 ч, первая, третья и четвертая - за 3 ч. Если же будут работать только первая и вторая бригады, то вагон будет разгружен за 6 ч. За какое время могут разгрузить вагон все четыре бригады, работая вместе?

Решение заданий работы

Часть 1

1. Оценим число . Так как 81 < 91 < 100, то Поэтому числу соответствует точка Р.

Ответ: 3.

2. Учтем, что 1/4 учащихся школы составляет 1/4 · 100 = 25% учащихся школы. Поэтому 26% учащихся школы больше, чем 1/4.

Ответ: 1.

3. Число a - нечетное. Поэтому число 2a - четное, т. к. кратно 2. Число a + 2 - нечетное, т. к. после а число a + 1 - четное, значит, следующее a + 2 - нечетное. Число a - 1 - четное, т. к. предшествует нечетному числу а. Число а2 + 1 - четное, т. к. следует после нечетного числа а2.

Итак, только число а + 2- нечетное.

Ответ: 2.

4. Так как тетрадь стоит а руб., то n тетрадей стоят аn руб. Пусть блокнот стоит х руб., тогда m блокнотов стоят хm руб. Общая стоимость покупки с руб. Получаем уравнение аn + хm = с.

Отсюда хm = с - аn и

Ответ: 4.

5. Дробное выражение имеет смысл, если его знаменатель не равен нулю. Найдем, при каких значениях переменной х данное выражение имеет смысл:

1) выражение (х + 1)(х - 1) имеет смысл при любых значениях х, т. е. 1 → г;

2) выражение имеет смысл при х ≠ ±1, т. к. при таких х знаменатель дроби не равен нулю, т. е. 2 → в;

3) выражение имеет смысл при х ≠ 1, т. к. при таких х знаменатель дроби не равен нулю, т. е. 3 → б;

4) выражение имеет смысл при х ≠ -1, т. к. при таких х знаменатель дроби не равен нулю, т. е. 4 → а.

Ответ: 1 → г; 2 → в; 3 → б; 4 → а.

6. Разложим числитель и знаменатель дроби на множители и сократим ее. В числителе дроби вынесем общий множитель за скобки, в знаменателе используем формулу квадрата разности и получим:

Ответ:

7. Используя свойства степеней, упростим выражение Подставим величину и получим:

Ответ: 1.

8. Если в выражении (x - 2)(х - 3) одновременно изменить знаки каждого множителя, то результат умножения не изменится. Поэтому (х - 2)(х - 3) = (2 - х)(3 - х).

Ответ: 1.

9. Для квадратного уравнения x2 + 2х - 3 = 0 найдем D/4 = 1 + 3 = 4 и корни т. е. x1 = 1 и х2 = -3.

Ответ: x1 = 1 и х2 = -3.

10. Из рисунка видно, что парабола и прямая пересекаются в двух точках, координаты которых (-3; 5) и (2; 0), что и является решениями данной системы уравнений.

Ответ: (-3; 5), (2; 0).

11. Пусть за 1 ч внук пропалывал х грядок, тогда бабушка пропалывала х - 2 грядки. Внук прополет 14 грядок за 14/x ч, а бабушка прополет 15 грядок за ч. Всего на работу было затрачено 5 ч. Получаем уравнение

Ответ: 3.

12. Решим каждое неравенство отдельно и найдем решение системы линейных неравенств. Получим: 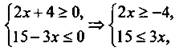откуда Поэтому решение системы неравенств х ≥ 5.

Ответ: 2.

13. Так как 0 < a < 1 (т. е. a — положительное число), то по свойству числовых неравенств 1/a > 1/1, или 1/a > 1. Поэтому a < 1/a.

Ответ: 2.

14. Так как разность d арифметической прогрессии равна 3, то в формулу n-го члена an будет входить слагаемое 3n.

Ответ: 3.

15. Проверим все данные утверждения. Неверно утверждение 4, что нулями функции являются числа -1,5; 2; 3,5, т. к. из графика видно, что функция имеет только два нуля.

Ответ: 4.

16. Из рисунка видно, что автомобиль проехал 200 км за 4 ч. Поэтому скорость его 200 : 4 = 50 км/ч. Автобус проехал 200 км за 5 ч и его скорость 200 : 5 = 40 км/ч. Поэтому скорость автомобиля на (50 - 40) = 10 км/ч больше скорости автобуса.

Ответ: на 10 км/ч.

Часть 2

17. (2). В системе уравнений 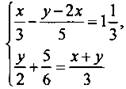все члены первого уравнения умножим на 15, второго - на 6 и получим: Умножим второе уравнение на (-3): и, сложив уравнения, получим 5х = 5, откуда х = 1. Подставим это значение в первое уравнение 11 - 3у = 20, откуда у = -3.

Ответ: (1; -3).

18. (4). Область определения выражения 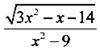задается условиями 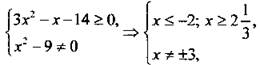поэтому х ≤ -2 и х ≠ -3; и х ≠ 3.

Ответ: х ≤ -2 и х ≠ -3; и х ≠ 3.

19. (4). Выпишем натуральные числа, кратные 3: 3, 6, 9, 12, ... Эти числа образуют арифметическую прогрессию с первым членом а1 = 3 и разностью d = 3. Найдем число членов, не превосходящих 200. Используя формулу n-го члена an = а1 + d(n - 1), получим неравенство 3 + 3(n - 1) ≤ 200, или 3n ≤ 200, откуда Поэтому таких чисел 66.

Используя формулу суммы n первых членов прогрессии найдем сумму таких чисел:

Ответ: 6633.

20. (6). Так как прямая 3х + 2у = с касается гиперболы у = 6/х в точке с положительными координатами, то система уравнений должна иметь единственное положительное решение.

Из первого уравнения выразим и подставим во второе: или сх - 3х2 = 12, или 0 = 3х - сх + 12. Чтобы это уравнение имело единственное решение, его дискриминант D = с2 - 4 · 3 · 12 = с2 - 122 = 0, откуда с = ±12. Найдем величину х. Подставим значения с = ±12 в уравнение 0 = 3х2 - сх + 12 и получим: 0 = 3х2 12х + 12 ⇒ 0 = х2 4х + 4 ⇒ 0 = (х 2)2. Положительное значение х = 2 получается при с = 12. Теперь найдем у = 6/x и получим у = 3.

Ответ: (2; 3).

21. (6). Примем всю работу за единицу. Введем производительность труда четырех бригад x, y, z и t соответственно.

По условиям задачи составим систему уравнени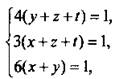й: или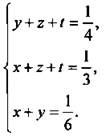

Сложим три уравнения системы: откуда

Тогда все четыре бригады, работая вместе, могут разгрузить вагон за время

Ответ: ч.