Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Некоторые приемы решения систем уравнений второй степени с двумя переменными (факультативное занятие) - Неравенства с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Цель: рассмотреть и систематизировать основные способы решения систем нелинейных уравнений.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Изобразите на координатной плоскости множество решений системы неравенств.
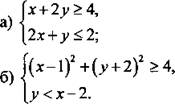
Вариант 2
Изобразите на координатной плоскости множество решений системы неравенств.
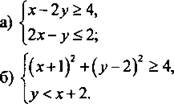
III. Изучение нового материала
Система уравнений, в которой хотя бы одно из уравнений не является линейным, называется системой нелинейных уравнений. Как вы видели, существуют способы решения любой системы линейных уравнений. Для систем нелинейных уравнений таких универсальных способов не существует, и многие системы до сих пор не решены.
Основной подход к решению систем линейных уравнений состоит в том, что с помощью тех или иных преобразований получают линейное уравнение, содержащее неизвестные. Это уравнение позволяет выразить одну неизвестную через другие и затем использовать для решения способ подстановки.
Остановимся на самых распространенных системах нелинейных уравнений.
а) Системы, содержащие одно линейное уравнение
Как правило, такие системы решаются способом подстановки. Из линейного уравнения одна из неизвестных выражается через другую и подставляется в оставшееся уравнение. Затем это уравнение с одной неизвестной решается, потом определяется и вторая неизвестная.
Пример 1
Решим систему уравнений 
Так как в системе второе уравнение является линейным, то выразим из него, например, неизвестную у = -(х + 8) и подставим ее в первое уравнение: х2 + (х + 8)2 + 6х - 2(х + 8) = 0, ИЛИ х2 + 10х + 24 = 0. Корни этого уравнения: x1 = -6 (и тогда у1 = -2) и х2 = -4 (у2 = -4). Итак, система имеет два решения: (-6; -2), (-4; -4).
Пример 2
Решим систему уравнений 
В данной системе линейного уравнения нет, но оно легко может быть получено из первого уравнения. Введем замену: ![]() и получим уравнение t + 6/t = 5, корни которого t1 = 2, t2 = 3. В первом случае имеем:
и получим уравнение t + 6/t = 5, корни которого t1 = 2, t2 = 3. В первом случае имеем: ![]() или х = 3у. Тогда получаем систему:
или х = 3у. Тогда получаем систему: 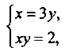 которая имеет решения:
которая имеет решения: 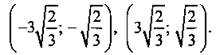 Во втором случае:
Во втором случае: ![]() или х = 2у. Тогда получаем систему:
или х = 2у. Тогда получаем систему: 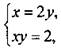 которая имеет решения: (-2; -1), (2; 1). Таким образом, исходная система имеет четыре решения,
которая имеет решения: (-2; -1), (2; 1). Таким образом, исходная система имеет четыре решения,
б) Системы, которые с помощью замен сводятся к линейным
Пример 3
Решим систему уравнений 
Введем замены неизвестных: ![]() и получим систему линейных уравнений
и получим систему линейных уравнений ![]() Эта система имеет единственное решение: u = 1, v = 1. Возвращаясь к неизвестным х и у, опять получим систему линейных уравнений:
Эта система имеет единственное решение: u = 1, v = 1. Возвращаясь к неизвестным х и у, опять получим систему линейных уравнений: ![]() или
или ![]() Эта система имеет единственное решение: х = 1 ,у = 1.
Эта система имеет единственное решение: х = 1 ,у = 1.
Пример 4
Решим систему уравнений 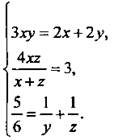
Подсказкой в данном примере служит третье уравнение. Легко сообразить, что первое и второе уравнения могут быть приведены к аналогичному виду. Например, для второго уравнения необходимо сделать следующие преобразования: ![]()
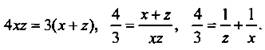 Таким образом, имеем систему уравнений:
Таким образом, имеем систему уравнений: 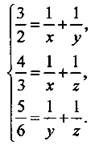 Теперь замена неизвестных очевидна:
Теперь замена неизвестных очевидна: ![]() В результате получаем систему линейных уравнений
В результате получаем систему линейных уравнений 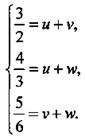 Характерной особенностью полученной системы является то, что в ней неизвестные u, v, w входят по два раза. Поэтому удобно сложить все три уравнения системы:
Характерной особенностью полученной системы является то, что в ней неизвестные u, v, w входят по два раза. Поэтому удобно сложить все три уравнения системы: ![]() откуда
откуда ![]() Вычитая из этого соотношения каждое из уравнений системы, соответственно, получим:
Вычитая из этого соотношения каждое из уравнений системы, соответственно, получим: ![]() После этого легко найти исходные неизвестные:
После этого легко найти исходные неизвестные: ![]() Таким образом, система имеет единственное решение: (1; 2; 3).
Таким образом, система имеет единственное решение: (1; 2; 3).
в) Однородные системы
Системы уравнений, у которых левая часть одного из уравнений является однородным многочленом, а правая часть равна нулю, или, у которых левые части двух уравнений являются однородными многочленами, а правые части равны числам, не равным нулю, называются однородными системами уравнений.
Пример 5
Решим систему уравнений 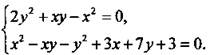
Первое уравнение этой системы является однородным (слева стоит однородный многочлен второй степени по переменным х и у, справа - ноль). Решим его относительно неизвестной у, считая х постоянной величиной, и получим: у = -х и у = x/2. Подставим полученное соотношение во второе уравнение. В случае y = -х имеем: х2 - х(-х) - (-х)2 + 3х + 7(-х) + 3 = 0, или х2 - 4х + 3 = 0. Тогда: х1 = 1, y1 = -1, х2 = 3, у2 = -3. В случае y = x/2 получаем: ![]() или х2 + 26х + 12 = 0. Тогда:
или х2 + 26х + 12 = 0. Тогда: ![]() Итак, система уравнении имеет четыре решения.
Итак, система уравнении имеет четыре решения.
Пример 6
Решим систему уравнений 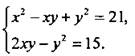
Левые части уравнения представляют собой однородные многочлены второй степени, что позволяет свести задачу к предыдущей. Необходимо только избавиться от чисел в правой части. Для этого умножим первое уравнение на 5, получим: 5х2 - 5ху + 5у2 = 105, второе - на (-7), получим: -14ху + 7у2 = -105. Полученные уравнения сложим: 12у2 - 19ху + 5х2 = 0. Решая это уравнение, найдем: у = 5/4х и у = x/3. Для нахождения х можно использовать любое из уравнений исходной системы, например второе. В случае у = 5/4х имеем: ![]() или х2 = 16. Тогда: x1 = -4, у1 = -5; х2 = 4, у2 = 5. В случае y = x/3 получаем:
или х2 = 16. Тогда: x1 = -4, у1 = -5; х2 = 4, у2 = 5. В случае y = x/3 получаем: ![]() или x2 = 27. Тогда:
или x2 = 27. Тогда: ![]() Даная система уравнений также имеет четыре решения.
Даная система уравнений также имеет четыре решения.
г) Симметричные системы
Система уравнений называется симметричной, если при замене х на у, а у на х уравнения системы не меняются. Для решения симметричных систем в качестве новых переменных используют простейшие симметричные выражения: u = х + у, v = ху (способ замены неизвестных).
Пример 7
Решим систему уравнений 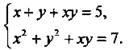
Система уравнений 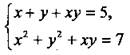 является симметричной, т. к. при замене х на у, а у на х получаем систему
является симметричной, т. к. при замене х на у, а у на х получаем систему 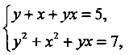 которая с точностью до перестановки слагаемых и сомножителей совпадает с исходной.
которая с точностью до перестановки слагаемых и сомножителей совпадает с исходной.
Введем новые неизвестные: u = х + у, v = ху. Учтем, что х2 + у2 = (х + у)2 - 2ху = u2 - 2v. Тогда исходная система будет иметь вид: ![]() Сложив уравнения системы, получим квадратное уравнение для определения u: u2 + u - 12 = 0, откуда u1 = -4, u2 = 3. Тогда v1 = 9, v2 = 2. Возвращаясь к старым неизвестным, получаем системы:
Сложив уравнения системы, получим квадратное уравнение для определения u: u2 + u - 12 = 0, откуда u1 = -4, u2 = 3. Тогда v1 = 9, v2 = 2. Возвращаясь к старым неизвестным, получаем системы: ![]() и
и ![]() Решение этих систем труда не вызывает, т. к. первое уравнение в них линейное. Решая их, получим для первой системы - отсутствие решений, для второй - (1; 2), (2; 1).
Решение этих систем труда не вызывает, т. к. первое уравнение в них линейное. Решая их, получим для первой системы - отсутствие решений, для второй - (1; 2), (2; 1).
Заметим, что симметричность системы сказалась и на симметричности ответов: если симметричная система имеет решение (а; b), то она имеет и решение (b; а). В нашем случае были получены симметричные ответы (1; 2) и (2; 1).
Во многих случаях система, не являющаяся симметричной, с помощью соответствующих замен неизвестных может быть сведена к таковой.
Пример 8
Решим систему уравнений 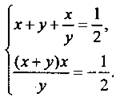
Введем новые неизвестные u = х + у, v = x/y и получим симметричную систему уравнений 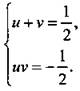 Решения этой системы:
Решения этой системы: ![]() Получаем системы уравнений:
Получаем системы уравнений: 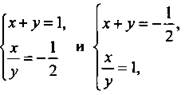 которые являются линейными. Решение первой системы: (-1; 2), второй: (-1/4; -1/4).
которые являются линейными. Решение первой системы: (-1; 2), второй: (-1/4; -1/4).
В заключение этой темы заметим, что при анализе или решении линейных или нелинейных систем уравнений полезно использовать графические методы.
Пример 9
Сколько решений имеет система уравнений 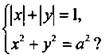
Записав первое уравнение в виде |у| = 1 - |х|, нетрудно построить его график. Им будет квадрат, отсекающий на осях координат единичные отрезки (сплошные линии). Графиком второго уравнения является окружность радиуса |а| с центром в начале координат (штрихпунктирные линии).
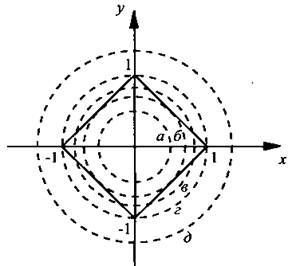
Из рисунка видны следующие возможные случаи: окружности a и д не имеют точек пересечения с квадратом, т. е. система не имеет решений: окружности б и г имеют с квадратом четыре общие точки, т. е. система имеет четыре решения; окружность в пересекает квадрат в восьми точках, т. е. система имеет восемь решений.
Установим, при каких значениях |а| имеют место эти случаи. Прежде всего отметим, что диагональ квадрата равна 2, а его сторона равна ![]() Из рисунка видно, что радиус окружности б равен половине стороны квадрата, т. е.
Из рисунка видно, что радиус окружности б равен половине стороны квадрата, т. е. ![]() Радиус окружности г равен половине диагонали квадрата, т. е. |а| = 1. Теперь можно записать ответ: при
Радиус окружности г равен половине диагонали квадрата, т. е. |а| = 1. Теперь можно записать ответ: при 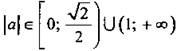 система решений не имеет, при
система решений не имеет, при 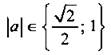 система имеет четыре решения, при
система имеет четыре решения, при 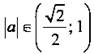 система имеет восемь решений.
система имеет восемь решений.
Отметим, что иногда встречаются и системы двух уравнений с тремя неизвестными. Рассмотрим подход к таким задачам.
Пример 10
Дана система уравнений 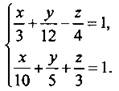 Найдем сумму неизвестных x + y + z.
Найдем сумму неизвестных x + y + z.
Умножим первое уравнение на 12, второе на 30. Получим систему уравнений ![]() Сложим уравнения системы, получим: 7х + 7y + 7z = 42, откуда х + у + z = 6. Сумма неизвестных найдена: х + у + z = 6. При этом сами неизвестные (по отдельности) найти невозможно.
Сложим уравнения системы, получим: 7х + 7y + 7z = 42, откуда х + у + z = 6. Сумма неизвестных найдена: х + у + z = 6. При этом сами неизвестные (по отдельности) найти невозможно.
Пример 11
Решим систему уравнений 
В первом уравнении системы выделим квадраты разности по переменным х и у: (х2 - 8х + 16) + (у2 - 2у + 1) = -17 + 17, или (х - 4)2 + (у - 1)2 = 0. Каждое слагаемое в этой сумме неотрицательное. Поэтому равенство выполняется только при х - 4 = 0 и у - 1 = 0, откуда х = 4 и у = 1. Подставим эти значения во второе уравнение системы: 3z - 4 + 5 · 1 = -8, или 3z = -9, откуда z = -3. Итак, данная система имеет единственное решение: х = 4, у = 1, z = -3.
Заметим, что во многих случаях решение системы уравнений вызывает очень большие трудности и требует значительной наблюдательности и навыков решения самых различных задач.
Пример 12
Решим систему уравнений 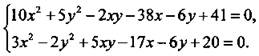
Умножим второе уравнение системы на 2 и получим: 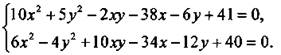 Сложим и вычтем уравнения и получим равносильную систему уравнений:
Сложим и вычтем уравнения и получим равносильную систему уравнений:  или
или 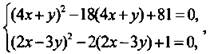 или
или 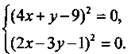 Такая система равносильна системе линейных уравнений
Такая система равносильна системе линейных уравнений 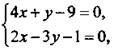 которая имеет единственное решение: х = 2, y = 1.
которая имеет единственное решение: х = 2, y = 1.
IV. Контрольные вопросы
1. Как решаются системы, содержащие линейное уравнение?
2. Дайте определение однородной системы уравнений.
3. Решение однородных систем уравнений.
4. Определение симметричной системы уравнений.
5. Как решаются симметричные системы уравнений?
V. Задание на уроке
№ 507 (а); 508 (б); 509 (а); 510 (б); 511 (а); 512 (б); 513 (а); 514 (б); 515(a).
VI. Задание на дом
№ 507 (б); 508 (а); 509 (б); 510 (а); 511 (б); 512 (а); 513 (б); 514 (а); 515 (б).
VII. Творческие задания
Решите системы рациональных уравнений.
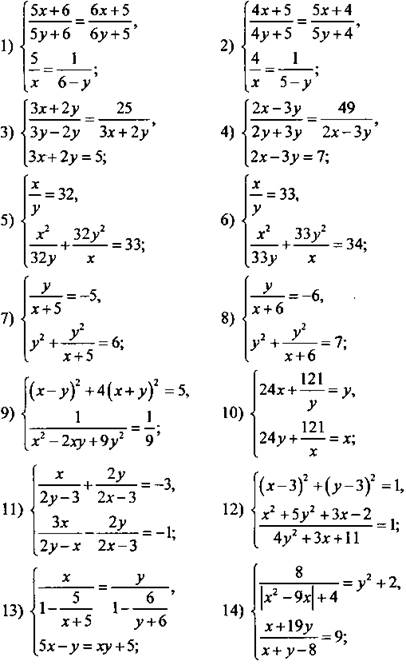
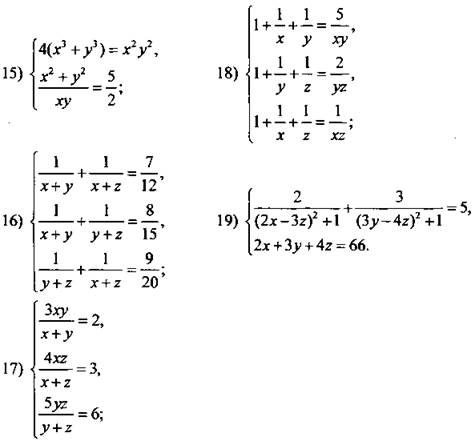
Найдите все пары (x; у) целых чисел хну, которые являются решениями системы уравнений.
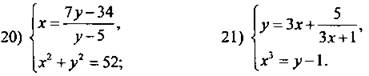
Решите системы иррациональных уравнений.

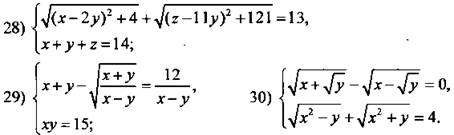
Ответы: ![]()
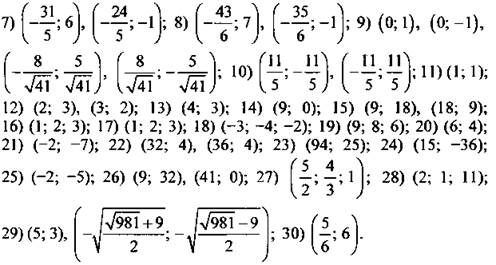
VIII. Подведение итогов урока