Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Решение задач с помощью систем уравнений второй степени - Уравнения с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Целы использовать системы уравнений для решения текстовых задач.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
Вариант 1
1. Способом подстановки решите систему уравнений.

Ответы: ![]()
![]()
2. Способом сложения решите систему уравнений.
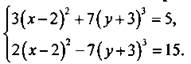
Ответы: а) (0; -4), (4; -4); б) (4; -4); в) (2; -4); г) (4; -6).
Вариант 2
1. Способом подстановки решите систему уравнений.
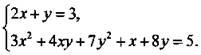
Ответы: а) (2; -1); б) (2; -1), (41/23; -13/23); в) (2; -1), (34; -65); г) (2; -1), (18; -33).
2. Способом сложения решите систему уравнений.
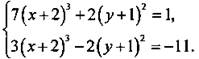
Ответы: а) (-3; 1); б) (-3; 2); в) (-3; -3); г) (-3; 1), (-3; -3).
III. Изучение нового материала
Системы уравнений с двумя неизвестными часто используются при решении текстовых задач.
Пример 1
Произведение двух чисел равно 168, а сумма их квадратов равна 340. Найдите эти числа.
Пусть одно из чисел х, другое у. Запишем условия задачи и получим систему уравнений 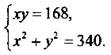
Решим эту систему двумя способами.
1-й способ - способ подстановки.
Из первого уравнения выразим у = 168/x и подставим во второе уравнение.
Получим: х2 + (168/x)2 = 340, или х4 – 340x2 + 28 224 = 0.
Корни этого биквадратного уравнения: x1,2 = ±12 и х3,4 = ±14.
По формуле y = 168/x найдем соответствующие значения у: y1,2 = ±14 и y3,4 = ±12.
Итак, задача имеет четыре решения: (12; 14), (-12; -14), (14; 12), (-14;-12).
2-й способ - способ сложения.
Умножим первое уравнение на 2 и запишем систему уравнений в виде 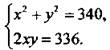 Сложим и вычтем уравнения системы. Получим:
Сложим и вычтем уравнения системы. Получим: 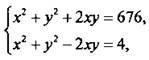 или
или  или
или 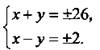
Таким образом, данная система сводится к четырем системам линейных уравнений:
а) 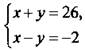 - решение (12; 14);
- решение (12; 14);
б) 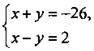 - решение (-12; -14);
- решение (-12; -14);
в) ![]() - решение (14; 12);
- решение (14; 12);
г) 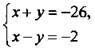 - решение (-14; -12).
- решение (-14; -12).
Пример 2
Периметр прямоугольного треугольника равен 30 см, а его гипотенуза равна 13 см. Найдите стороны треугольника.
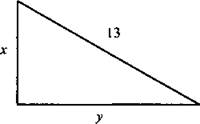
Пусть катеты треугольника равны jc см и у см. Используя теорему Пифагора, запишем условия задачи:
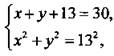 или
или 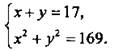
Решим эту систему способом подстановки. Из первого уравнения выразим у = 17 - х и подставим во второе уравнение. Получим квадратное уравнение х2 + (17 - x)2 = 169, или x2 - 17x + 60 = 0, корни которого: x1 = 5 и x2 = 12. По формуле у = 17 - x найдем соответствующие значения у: у1 = 12 и у2 = 5.
Итак, длины катетов равны 5 и 12 см.
IV. Задание на уроке
№ 455; 457; 460; 461; 463; 467; 469; 476.
V. Задание на дом
№ 456; 458; 459; 462; 464; 468; 470; 473; 477.
VI. Подведение итогов урока
§ 8. Неравенства с двумя переменными и их системы