Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Графический способ решения систем уравнений - Уравнения с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Цель: использовать графики для решения систем уравнений.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Определение решения уравнения с двумя переменными.
2. Постройте график уравнения.
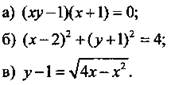
Вариант 2
1. Определение уравнения с двумя переменными.
2. Постройте график уравнения.
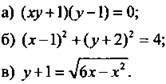
III. Изучение нового материала
Рассмотрим систему двух уравнений с двумя неизвестными. Решением системы уравнений называют пару значений переменных, которые обращают каждое уравнение системы в верное равенство. Решить систему уравнений означает, найти все ее решения или доказать, что решений нет.
Одним из эффективных и наглядных способов решения и исследования уравнений и систем уравнений является графический способ.
Пример 1
Решим систему уравнений 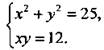
Построим в одной системе координат графики первого х2 + у2 = 25 (окружность) и второго ху = 12 (гипербола) уравнений. Видно, что графики уравнений пересекаются в четырех точках A(3; 4), В(4; 3), С(-3; -4) и D(-4; 3), координаты которых являются решениями одной системы.
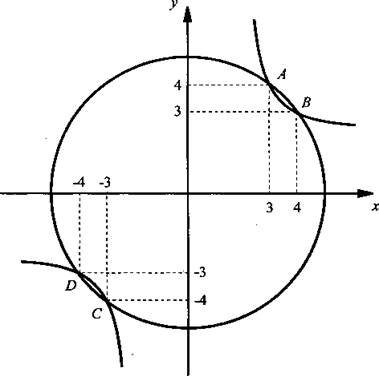
Так как при графическом способе решения могут быть найдены с некоторой точностью, то их необходимо проверить подстановкой. Проверка показывает, что система действительно имеет четыре решения: (3; 4), (4; 3), (-3; -4), (-4; -3).
Пример 2
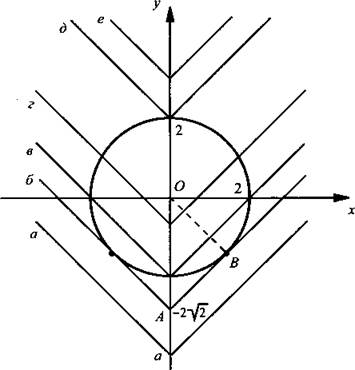
При всех значениях параметра а определим число решений системы уравнении 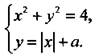
Построим график первого уравнения х2 + у2 = 22 (окружность) и второго уравнения у = |х| + а для различных значений параметра а. Этот график пересекает ось ординат в точке у = а. Из прямоугольного равнобедренного треугольника ОАВ найдем гипотенузу ![]() Тогда сразу получаем ответ задачи: при
Тогда сразу получаем ответ задачи: при ![]() система не имеет решений (графики а, е), при
система не имеет решений (графики а, е), при ![]() система имеет два решения (графики б, г), при a = -2 - три решения (график в) и при a = 2 - одно решение (график д).
система имеет два решения (графики б, г), при a = -2 - три решения (график в) и при a = 2 - одно решение (график д).
Пример 3
При каких значениях параметра а система уравнений 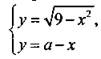 имеет единственное решение?
имеет единственное решение?
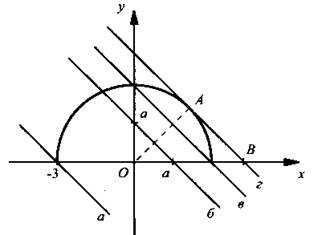
Построим график первого уравнения ![]() (верхняя полуокружность, т. к. у ≥ 0). Также в этой системе координат строим график второго уравнения у = а - х для различных значений параметра а (прямая). Эта прямая пересекает оси координат в точках х = а и у = а. Очевидно, что система уравнений имеет единственное решение, если прямая у = а - х находится между положениями а и b, а также в случае касания г. Для этого случая из прямоугольного равнобедренного треугольника ОАВ найдем гипотенузу
(верхняя полуокружность, т. к. у ≥ 0). Также в этой системе координат строим график второго уравнения у = а - х для различных значений параметра а (прямая). Эта прямая пересекает оси координат в точках х = а и у = а. Очевидно, что система уравнений имеет единственное решение, если прямая у = а - х находится между положениями а и b, а также в случае касания г. Для этого случая из прямоугольного равнобедренного треугольника ОАВ найдем гипотенузу ![]() (соответственно
(соответственно ![]() ). Следовательно, при
). Следовательно, при ![]() система уравнений имеет единственное решение.
система уравнений имеет единственное решение.
IV. Задание на уроке
№ 415 (б); 416; 419 (а); 420 (б); 421 (а, б); 422 (а); 424 (б); 426.
V. Задание на дом
№ 415 (б); 417; 418; 419 (б); 420 (а); 421 (б, г); 422 (б); 424 (а); 425; 427.
VI. Творческие задания
1. Найдите значения параметра а, при которых система уравнений имеет ровно два решения.
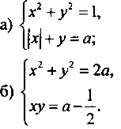
Ответы: ![]()
2. Найдите значения параметра а, при которых система уравнений имеет ровно три решения.
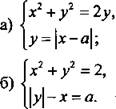
Ответы: ![]()
3. Для каждого значения параметра а определите число решений системы уравнений.
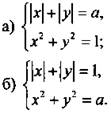
Ответы: а) при ![]() - нет решений,
- нет решений, ![]() - четыре решения, при
- четыре решения, при ![]() - восемь решений;
- восемь решений;
б) при 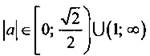 _ нет решений, при
_ нет решений, при  - четыре решения, при
- четыре решения, при  - восемь решений.
- восемь решений.
VII. Подведение итогов урока