Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Итоги контрольной работы - Степенная функция. Корень n-й степени - Квадратичная функция
Цель: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.
Ход урока
I. Сообщение темы и цели урока
II. Итоги контрольной работы
III. Ответы и решени.
Ответы
Вариант 1
1. Ответ: D(y) = [2; +∞), Е(у) = [4; +∞).
2. Ответ: (х - 1)(5х - 2).
3. Ответ: уmax = 8 при х = -1.
4. Ответ: график построен.
5. Ответ: 4.
Вариант 2
1. Ответ: D(y) = [2; +∞), Е(у) = [1; +∞).
2. Ответ: (х - 1)(7х - 5).
3. Ответ: уmах = -5 при х = 1.
4. Ответ: график построен.
5. Ответ: -2.
Вариант 3
1. Ответ: D(y) = [2; +∞), Е(у) = [6; +∞).
2. Ответ: а(6х2 - х - 2), где а ≠ 0.
3. Ответ: уmах = 9 при х = 3.
4. Ответ: график построен.
5. Ответ: 4.
Вариант 4
1. Ответ: D(y) = [2; +∞), Е(у) = [-1; +∞).
2. Ответ: a(6x2 - х - 1), где а ≠ 0.
3. Ответ: уmax = 5 при х = 2.
4. Ответ: график построен.
5. Ответ: 6.
Решени.
Вариант 5
1. Область определения функции ![]() задается неравенством 3х - 6 ≥ 0, откуда х ≥ 2 и D(y) = [2; +∞). Функции
задается неравенством 3х - 6 ≥ 0, откуда х ≥ 2 и D(y) = [2; +∞). Функции ![]() и у2 = 2х2 + 4х - 5 на промежутке [2; +∞) возрастают. Найдем у(2) = 4 · 0 + 2 · 4 + 4 · 2 - 5 = 11. Поэтому область значений данной функции Е(у) = [11; +∞).
и у2 = 2х2 + 4х - 5 на промежутке [2; +∞) возрастают. Найдем у(2) = 4 · 0 + 2 · 4 + 4 · 2 - 5 = 11. Поэтому область значений данной функции Е(у) = [11; +∞).
Ответ: D(y) = [2; +∞), Е(у) = [11; +∞).
2. Для квадратного трехчлена 2х2 - 3х - 1 запишем формулы Виета: х1 + х2 = 3/2 и х1х2 = -1/2. Пусть искомый трехчлен имеет вид: ay2 + by + с и корни y1 и у2. Запишем для них формулы Виета: ![]() (откуда b = -7/2а) и
(откуда b = -7/2а) и ![]() (откуда с = 2а). Тогда искомый трехчлен имеет вид:
(откуда с = 2а). Тогда искомый трехчлен имеет вид: ![]()
![]() где а ≠ 0.
где а ≠ 0.
Ответ: ![]() где а ≠ 0.
где а ≠ 0.
3. В данной функции ![]() выделим целую часть и запишем ее в виде
выделим целую часть и запишем ее в виде 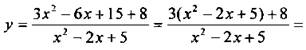
![]() Наибольшее значение функция у достигает, если второе слагаемое максимально, т. е. знаменатель дроби минимальный. Это имеет место при х = 1 и уmax = 3 + 8/4 = 5.
Наибольшее значение функция у достигает, если второе слагаемое максимально, т. е. знаменатель дроби минимальный. Это имеет место при х = 1 и уmax = 3 + 8/4 = 5.
Ответ: уmах = 5 при х = 1.
4(a). Очевидно, что функция у = х2 - 5|х| + 4 четная и ее график симметричен относительно оси ординат. При х ≥ 0 функция имеет вид: у = х2 - 5х + 4. График пересекает ось ординат в точке у = 4 и ось абсцисс в точках x1 = 1 и х2 = 4. Вершина параболы имеет координаты (2,5; -2,25). Строим этот график при х ≥ 0 и симметрично отражаем его влево.
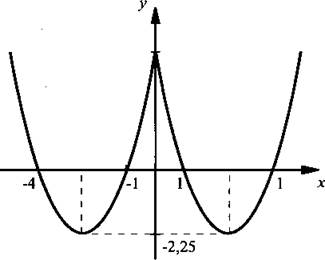
Ответ: график построен.
4(б). Раскроем знак модуля и запишем функцию ![]() в виде
в виде 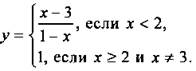 При х < 2 строим гиперболу
При х < 2 строим гиперболу ![]() Она пересекает ось ординат в точке у = -3, имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = -1. При х ≥ 2 и х ≠ 3 строим прямую у = 1.
Она пересекает ось ординат в точке у = -3, имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = -1. При х ≥ 2 и х ≠ 3 строим прямую у = 1.
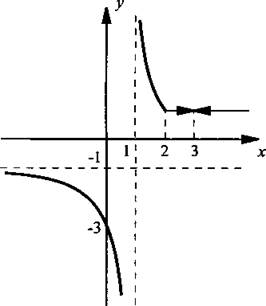
Ответ: график построен.
5. Чтобы упростить выражение ![]() удобно ввести новую переменную
удобно ввести новую переменную ![]() тогда у2 = х + 1 и х = у2 - 1. Выражение имеет вид:
тогда у2 = х + 1 и х = у2 - 1. Выражение имеет вид: ![]()
Ответ: 6.
Вариант 6
1. Область определения функции ![]() задается неравенством 2х - 4 ≥ 0, откуда х ≥ 2 и D(у) = [2; +∞). Функции
задается неравенством 2х - 4 ≥ 0, откуда х ≥ 2 и D(у) = [2; +∞). Функции ![]() и у2 = 4х2 - 8х + 5 на промежутке [2; +∞) возрастают. Найдем у(2) = 3 · 0 + 4 · 4 – 8 · 2 + 5 = 5. Поэтому область значений данной функции Е(у) = [5; +∞).
и у2 = 4х2 - 8х + 5 на промежутке [2; +∞) возрастают. Найдем у(2) = 3 · 0 + 4 · 4 – 8 · 2 + 5 = 5. Поэтому область значений данной функции Е(у) = [5; +∞).
Ответ: D(у) = [2; +∞), Е(у) = [5; +∞).
2. Для квадратного трехчлена 3х2 - 5х + 1 запишем формулы Виета: х1 + х2 = 5/3 и х1х2 = 1/3. Пусть искомый трехчлен имеет вид: ay2 + by + c и корни у1 и у2. Запишем для них формулы Виета: ![]() (откуда b = 1/3а) и
(откуда b = 1/3а) и ![]() (откуда с = -1/3а). Тогда искомый трехчлен имеет вид:
(откуда с = -1/3а). Тогда искомый трехчлен имеет вид: ![]()
![]() , где а ≠ 0.
, где а ≠ 0.
Ответ: ![]() .
.
3. В данной функции ![]() выделим целую часть и запишем ее в виде
выделим целую часть и запишем ее в виде ![]()
![]() Наименьшее значение функция у достигает, если вычитаемое максимально, т. е. знаменатель дроби минимальный. Это имеет место при х = -1 и уmах = 5 – 6/3 = 3.
Наименьшее значение функция у достигает, если вычитаемое максимально, т. е. знаменатель дроби минимальный. Это имеет место при х = -1 и уmах = 5 – 6/3 = 3.
Ответ: уmах = 3 при х = -1.
4(a). Очевидно, что функция у = х2 - 4|х| + 3 четная и ее график симметричен относительно оси ординат. При х ≥ 0 функция имеет вид: у = х2 - 4х + 3. График пересекает ось ординат в точке у = 3 и ось абсцисс в точках x1 = 1 и х2 = 3. Вершина параболы имеет координаты (2; -1). Строим этот график при х ≥ 0 и симметрично отражаем его влево.
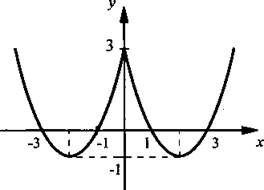
Ответ: график построен.
4(б). Раскроем знак модуля и запишем функцию ![]() в виде
в виде  При х < 1 строим гиперболу
При х < 1 строим гиперболу ![]() Она пересекает ось ординат в точке у = 3, имеет вертикальную асимптоту х = -1 и горизонтальную асимптоту у = -1. При х ≥ 1 и х ≠ 3 строим прямую у = 1.
Она пересекает ось ординат в точке у = 3, имеет вертикальную асимптоту х = -1 и горизонтальную асимптоту у = -1. При х ≥ 1 и х ≠ 3 строим прямую у = 1.
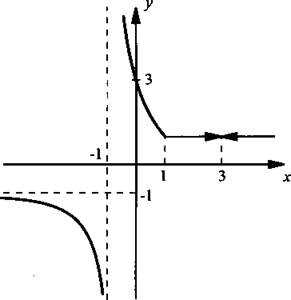
Ответ: график построен.
5. Чтобы упростить выражение ![]() удобно ввести новую переменную
удобно ввести новую переменную ![]() тогда у2 = х - 3 и х = у2 + 3. Выражение имеет вид:
тогда у2 = х - 3 и х = у2 + 3. Выражение имеет вид: 
Ответ: 2.