Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Степень с рациональным показателем (факультативное занятие) - Степенная функция. Корень n-й степени - Квадратичная функция
Цель: рассмотреть определение и свойства степени с рациональным показателем.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Постройте график функции.
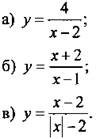
Вариант 2
Постройте график функции.
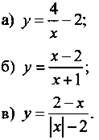
III. Изучение нового материала
Разумно считать, что выражение а1/n (где а > 0 и n – натуральное число) обозначает 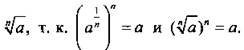 Это соображение позволяет определить степень с рациональным показателем: если а - положительное число, m/n - дробное число (где m - целое, n - натуральное число), то
Это соображение позволяет определить степень с рациональным показателем: если а - положительное число, m/n - дробное число (где m - целое, n - натуральное число), то ![]()
Пример 1
По определению степени с рациональным показателем имеем:
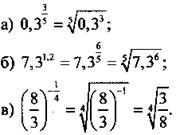
Степень с основанием, равным нулю, определена только для положительного дробного показателя и равна нулю, т. е. если m/n - положительное дробное число (m и n - натуральные числа), то 0m/n = 0. Для отрицательных оснований степень с дробным показателем не определена (не имеет смысла).
Пример 2
а) Выражения ![]() равны нулю.
равны нулю.
б) Выражения ![]() не имеют смысла.
не имеют смысла.
Свойства степени с целым показателем справедливы и для степени с рациональным показателем.
Для любого а > 0 и любых рациональных чисел р и q справедливы равенства:
![]()
Для любых а > 0 и b > 0 и любого рационального числа р выполнены равенства:
![]()
Пример 3
Найдем значение выражения ![]() при х = 30.
при х = 30.
Предварительно упростим это выражение. Получаем: ![]()
![]()
![]()
Подставим в полученное выражение ![]() значение х = 30 и найдем
значение х = 30 и найдем ![]()
Заметим, что можно избавиться от рациональных показателей степени. Для этого достаточно ввести новую переменную у = х0,5. Тогда данное выражение имеет вид: ![]()
![]()
![]() .
.
Так как х = у2 = 30, то сразу найдем ![]()
IV. Контрольные вопросы
1. Определение степени с рациональным показателем.
2. Свойства степени с рациональным показателем.
V. Задание на уроке
№ 190 (г); 191 (а, б, ж); 192 (в, д, ж); 193 (г, д, е); 194 (а, б); 195 (в, г); 196 (а); 197 (а, в, д); 198 (а); 199.
VI. Задание на дом
№ 190 (в); 191 (в, г, е, з); 192 (г, з); 193 (в, ж, и); 194 (в, г); 195 (а, б); 196 (б); 196 (б); 197 (б, г, е); 198 (б).
VII. Подведение итогов урока