Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Решение систем неравенств с одной переменной - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА
Цель: рассмотреть решение систем неравенств и двойных неравенств с одной переменной.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Аналитически решите неравенство: a(x - 1) ≤ 2(x - 1).
2. Аналитически и графически решите неравенство: |х + 2| - 2x – 6 ≥ 0.
Вариант 2
1. Аналитически решите неравенство: a(x - 1) ≥ 3(1 - x).
2. Аналитически и графически решите неравенство: |х - 1| - 3х – 6 ≤ 0.
III. Изучение нового материала (основные понятия)
Во многих случаях приходится иметь дело не с одним неравенством, а с системой неравенств с одной переменной. Решением системы неравенств с одной переменной называется значение переменной, при котором выполняется каждое неравенство системы. Решить систему неравенств означает найти все ее решения или доказать, что решений нет.
Пример 1
Рассмотрим систему неравенств ![]()
Число х = 3 является решением такой системы, т. к. при подстановке такого значения в неравенства системы получаем верные числовые неравенства (т. е. неравенства системы выполняются) ![]() Число х = -3 не является решением системы, т. к. при подстановке в систему такого значения первое неравенство выполняется, а второе — нет:
Число х = -3 не является решением системы, т. к. при подстановке в систему такого значения первое неравенство выполняется, а второе — нет: ![]()
Пример 2
Рассмотрим систему неравенств 
Такая система решений не имеет, т. к. не имеет решений второе неравенство (в этом легко убедиться, построив график левой части этого неравенства).
Для решения системы неравенств необходимо:
1) решить каждое неравенство в отдельности, т. е. найти множество решений такого неравенства;
2) найти пересечение этих множеств, которое и будет решением системы неравенств.
Пример 3
Решим систему неравенств ![]()
Будем параллельно решать каждое из неравенств системы. Получаем: ![]() или
или ![]() откуда
откуда ![]() На координатной оси изобразим решения первого (вверху) и второго (внизу) неравенств.
На координатной оси изобразим решения первого (вверху) и второго (внизу) неравенств.
![]()
Из рисунка видно, что пересечением множества решений неравенств является промежуток [2; 6), т. е. оба неравенства системы выполняются на этом промежутке. Поэтому промежуток [2; 6) является решением данной системы неравенств.
Заметим, что далеко не всегда необходимо решать все неравенства системы. В раде случаев достаточно решить самое простое неравенство и проверить выполнение других неравенств системы для найденного решения.
Пример 4
Решить систему неравенств 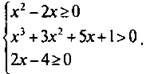
Заметим, что первое неравенство имеет вторую степень (квадратное неравенство), второе неравенство — третью степень (кубическое неравенство), третье неравенство — первую степень (линейное неравенство). Решение квадратных и кубических неравенств в 8-м классе не изучается. Поэтому решим последнее линейное неравенство и запишем первое неравенство в другом виде. Получаем: 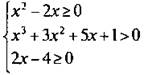 или
или 
Решение третьего неравенства — промежуток [2; +∞). Очевидно, что первое неравенство для таких х выполняется, т. к. в левой части оба множителя неотрицательны (т. е. х ≥ 2 и х -2 ≥ 0) и их произведение также неотрицательно. Второе неравенство при х ≥ 2 тоже выполняется, т. к. левая часть его содержит только положительные слагаемые (т. е. х3 > 0, 3х2 > 0, 5х > 0) и их сумма также положительна. Таким образом, решение данной системы неравенств — промежуток [2; +∞).
Часто к решению систем неравенств приводят двойные неравенства (далее в этом уроке будут рассмотрены только линейные неравенства).
Пример 5
Решим двойное неравенство ![]()
Заменим данное неравенство равносильной системой линейных неравенств ![]() и решим ее. Имеем:
и решим ее. Имеем: ![]() откуда
откуда  На числовой оси изобразим решение этих неравенств и найдем пересечение множеств этих решений — промежуток (3/4; 3]. Следовательно, решение данного двойного неравенства — промежуток (3/4; 3].
На числовой оси изобразим решение этих неравенств и найдем пересечение множеств этих решений — промежуток (3/4; 3]. Следовательно, решение данного двойного неравенства — промежуток (3/4; 3].
![]()
Заметим, что если крайние части двойного неравенства являются числами, то такое неравенство можно решить и проще (без сведения к системе неравенств). При этом используются свойства равносильности неравенств.
Пример 6
Решим двойное неравенство -3 ≤ 1 - 4х < 9.
По свойству равносильности из всех частей неравенства вычтем число 1. Получаем равносильное неравенство: ![]() или -4 ≤ -4х < 8. Разделим все части неравенства на отрицательное число -4 (при этом знаки неравенства меняются на противоположные) и получаем равносильное неравенство:
или -4 ≤ -4х < 8. Разделим все части неравенства на отрицательное число -4 (при этом знаки неравенства меняются на противоположные) и получаем равносильное неравенство: ![]() или 1 ≥ х > -2. Этот промежуток (-2; 1] является решением данного двойного неравенства. Для подобных примеров запись удобно вести следующим образом: -3 ≤ 1 - 4х < 9, -4 ≤ -4х < 8, 1 ≥ х > -2.
или 1 ≥ х > -2. Этот промежуток (-2; 1] является решением данного двойного неравенства. Для подобных примеров запись удобно вести следующим образом: -3 ≤ 1 - 4х < 9, -4 ≤ -4х < 8, 1 ≥ х > -2.
К системам неравенств очень часто приводят текстовые задачи.
Пример 7
Катер движется по реке, скорость которой 3 км/ч. Расстояние между пристанями составляет 100 км. При движении по течению реки катер проходит это расстояние менее чем за 4 часа, а при движении против течения — более чем за 5 часов. Какова собственная скорость катера?
Пусть собственная скорость катера х (км/ч), тогда скорость его по течению реки х + 3 (км/ч), против течения реки х - 3 (км/ч). По течению реки за 4 часа катер пройдет расстояние 4(х + 3) км и это расстояние будет более 100 км. Получаем неравенство 4(х + 3) > 100. Против течения реки за 5 часов катер пройдет расстояние 5(х - 3) км и это расстояние будет менее 100 км. Имеем неравенство 5(х - 3) < 100.
Для нахождения собственной скорости катера получили систему линейных неравенств ![]() Используя свойства равносильности неравенств, решим ее. Имеем:
Используя свойства равносильности неравенств, решим ее. Имеем: ![]() откуда
откуда ![]() Поэтому решение этой системы неравенств 22 < х < 23. Таким образом, собственная скорость катера более 22 км/ ч и менее 23 км/ч.
Поэтому решение этой системы неравенств 22 < х < 23. Таким образом, собственная скорость катера более 22 км/ ч и менее 23 км/ч.
IV. Контрольные вопросы
1. Что называется решением системы неравенств с одной переменной?
2. Что означает решить систему неравенств?
V. Задание на уроке
№ 820 (а, д); 823 (а); 825 (в); 827 (а); 829 (б); 830 (в); 834 (а); 836 (а); 838 (а); 840 (а).
VI. Задание на дом
№ 820 (б, е); 824 (б); 825 (г); 827 (г); 829 (в); 830 (г); 834 (б); 836 (г); 838 (б); 840 (б).
VII. Подведение итогов урока