Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Определение числовой функции и способы ее задания - Числовые функции - 1-е полугодие
Цель: обсудить определение функции, способы ее задания.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение материала 9 класса
Различные аспекты этой темы уже рассматривались в 7-9 классах. Теперь необходимо расширить и обобщить сведения о функциях. Напомним, что тема является одной из важнейших для всего курса математики. Различные функции будут изучаться вплоть до окончания школы и далее в высших учебных заведениях. Данная тема вплотную связана с решением уравнений, неравенств, текстовыми задачами, прогрессиями и т. д.
Определение 1. Пусть даны два множества действительных чисел D и Е и указан закон f по которому каждому числу х ∈ D ставится в соответствие единственное числом y ∈ Е (см. рисунок). Тогда говорят, что задана функция у = f(x) или у(х) с областью определения (О.О.) D и областью изменения (О.И.) Е. При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).

Область определения функции f обозначают D(f). Множество, состоящее из всех чисел f(x) (область значений функции f), обозначают E(f).
Пример 1
Рассмотрим функцию ![]() Для нахождения у для каждого значения х необходимо выполнить следующие операции: из величины х вычесть число 2 (х - 2), извлечь квадратный корень из этого выражения
Для нахождения у для каждого значения х необходимо выполнить следующие операции: из величины х вычесть число 2 (х - 2), извлечь квадратный корень из этого выражения ![]() и, наконец, прибавить число 3
и, наконец, прибавить число 3 ![]() Совокупность этих операций (или закон, по которому для каждого значения х ищется величина у) и называется функцией у(х). Например, для х = 6 находим
Совокупность этих операций (или закон, по которому для каждого значения х ищется величина у) и называется функцией у(х). Например, для х = 6 находим ![]()
![]() Таким образом, для вычисления функции у в данной точке х необходимо подставить эту величину х в данную функцию у(х).
Таким образом, для вычисления функции у в данной точке х необходимо подставить эту величину х в данную функцию у(х).
Очевидно, что для данной функции для любого допустимого числа х можно найти только одно значение у (т. е. каждому значению х соответствует одно значение у).
Рассмотрим теперь область определения и область изменения этой функции. Извлечь квадратный корень из выражения (х - 2) можно, только если эта величина неотрицательная, т. е. х - 2 ≥ 0 или х ≥ 2. Находим ![]() Так как по определению арифметического корня
Так как по определению арифметического корня ![]() то прибавим ко всем частям этого неравенства число 3, получим:
то прибавим ко всем частям этого неравенства число 3, получим: ![]() или 3 ≤ у < +∞. Находим
или 3 ≤ у < +∞. Находим ![]()
В математике часто используются рациональные функции. При этом функции вида f(x) = р(х) (где р(х) - многочлен) называют целыми рациональными функциями. Функции вида ![]() (где р(х) и q(x) - многочлены) называют дробно-рациональными функциями. Очевидно, дробь
(где р(х) и q(x) - многочлены) называют дробно-рациональными функциями. Очевидно, дробь ![]() определена, если знаменатель q(x) не обращается в нуль. Поэтому область определения дробно-рациональной функции
определена, если знаменатель q(x) не обращается в нуль. Поэтому область определения дробно-рациональной функции ![]() - множество всех действительных чисел, из которого исключены корни многочлена q(x).
- множество всех действительных чисел, из которого исключены корни многочлена q(x).
Пример 2
Рациональная функция ![]() определена при х - 2 ≠ 0, т. е. x ≠ 2. Поэтому область определения данной функции - множество всех не равных 2 действительных чисел, т. е. объединение интервалов (-∞; 2) и (2; ∞).
определена при х - 2 ≠ 0, т. е. x ≠ 2. Поэтому область определения данной функции - множество всех не равных 2 действительных чисел, т. е. объединение интервалов (-∞; 2) и (2; ∞).
Напомним, что объединением множеств А и В называется множество, состоящее из всех элементов, входящих хотя бы в одно из множеств А или В. Объединение множеств А к В обозначается символом АUВ. Так, объединением отрезков [1; 5] и (3; 9) является промежуток [1; 9). Объединение промежутков [1; 2) и [3; 4] (непересекающиеся промежутки) обозначают [1; 2) U [3; 4].
Возвращаясь к примеру, можно записать: ![]() Так как при всех допустимых значениях х дробь
Так как при всех допустимых значениях х дробь ![]() не обращается в нуль, то функция f(x) принимает все значения, кроме 3. Поэтому
не обращается в нуль, то функция f(x) принимает все значения, кроме 3. Поэтому ![]()
Пример 3
Найдем область определения дробно-рациональной функции ![]()
Знаменатели дробей обращаются в нуль при х = 2, х = 1 и х = -3. Поэтому область определения данной функции ![]()
Пример 4
Зависимость ![]() уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем: у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим: у = 12 + 1 = 2. Таким образом, одному значению x (x = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем: у = 2 · 1 - 3 = -1, а пользуясь нижней формулой, получим: у = 12 + 1 = 2. Таким образом, одному значению x (x = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
Пример 5
Приведены графики двух зависимостей y(x). Определим, какая из них является функцией.
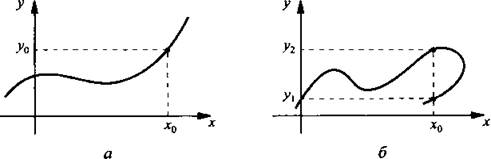
На рис. а приведен график функции, так как любой точке x0 соответствует только одно значение у0. На рис. б приведен график какой- то зависимости (но не функции), так как существуют такие точки (например,x0), которым отвечает более одного значения у (например, у1 и у2).
Рассмотрим теперь основные способы задания функций.
1) Аналитический (с помощью формулы или формул).
Пример 6
Рассмотрим функции: 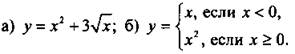
Несмотря на непривычную форму, это соотношение также задает функцию. Для любого значения х легко найти величину у. Например, для х = -0,37 (так как х < 0, то пользуясь верхним выражением), получаем: у(-0,37) = -0,37. Для х = 2/3 (так как х > 0, то пользуемся нижним выражением) имеем: ![]() Из способа нахождения у понятно, что любой величине х отвечает только одно значение у.
Из способа нахождения у понятно, что любой величине х отвечает только одно значение у.
в) 3х + у = 2у - х2. Выразим из этого соотношения величину у: 3х + х2 = 2у - у или х2 + 3х = у. Таким образом, это соотношение также задает функцию у = х2 + 3х.
2) Табличный
Пример 7
Выпишем таблицу квадратов у для чисел х.
x |
1 |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
6 |
7 |
y |
1 |
2,25 |
4 |
6,25 |
9 |
16 |
25 |
36 |
49 |
Данные таблицы также задают функцию - для каждого (приведенного в таблице) значения х можно найти единственное значение у. Например, у(1,5) = 2,25, y(5) = 25 и т. д.
3) Графический
В прямоугольной системе координат для изображения функциональной зависимости у(х) удобно пользоваться специальным рисунком - графиком функции.
Определение 2. Графиком функции y(x) называют множество всех точек системы координат, абсциссы которых равны значениям независимой переменной х, а ординаты - соответствующим значениям зависимой переменной у.
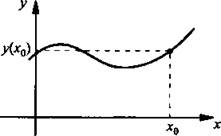
В силу такого определения все пары точек (х0, у0), которые удовлетворяют функциональной зависимости у(х), расположены на графике функции. Любые другие пары точек, не удовлетворяющие зависимости y(x), на графике функции не лежат.
Пример 8
Дана функция ![]() Принадлежит ли графику этой функции точка с координатами: а) (-2; -6); б) (-3; -10)?
Принадлежит ли графику этой функции точка с координатами: а) (-2; -6); б) (-3; -10)?
1. Найдем значение функции у при ![]()
![]() Так как у(-2) = -6, то точка А (-2; -6) принадлежит графику данной функции.
Так как у(-2) = -6, то точка А (-2; -6) принадлежит графику данной функции.
2. Определим значение функции у при ![]()
![]() Так как y(-3) = -11, то точка В (-3; -10) не принадлежит графику этой функции.
Так как y(-3) = -11, то точка В (-3; -10) не принадлежит графику этой функции.
По данному графику функции у = f(x) легко найти область определения D(f) и область значений E(f) функции. Для этого точки графика проецируют на оси координат. Тогда абсциссы этих точек образуют область определения D(f), ординаты - область значений E(f).
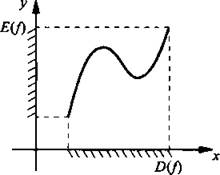
Сравним различные способы задания функции. Наиболее полным следует считать аналитический способ. Он позволяет составить таблицу значений функции для некоторых значений аргументов, построить график функции, провести необходимое исследование функции. Вместе с тем табличный способ позволяет быстро и легко найти значение функции для некоторых значений аргумента. График функции наглядно показывает ее поведение. Поэтому противопоставлять различные способы задания функции не следует каждый из них имеет свои преимущества и свои недостатки. На практике используются все три способа задания функции.
Будем считать основным аналитический способ задания функции и рассмотрим еще несколько задач.
Пример 9
Дана функция у = 2х2 - 3х +1.
Найдем: а) y(2); б) y(-3х); в) у(х + 1).
Для того чтобы найти значение функции при каком-то значении аргумента, необходимо подставить это значение аргумента в аналитический вид функции. Поэтому получим:
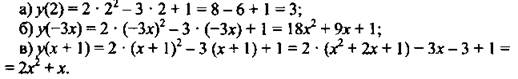
Пример 10
Известно, что у(3 - х) = 2х2 - 4. Найдем: а) y(x); б) у(-2).
а) Обозначим буквой z = 3-х, тогда х = 3 - z. Подставим это значение х в аналитический вид данной функции у(3 - х) = 2х2 - 4 и получим: y(3 - (3 - z)) = 2 · (3 - z)2 - 4, или y(z) = 2 · (3 - z)2 - 4, или y(z) = 2 · (9 - 6z + z2) - 4, или y(z) = 2х2 - 12z + 14. Так как безразлично, какой буквой обозначен аргумент функции - z, х, t или любой другой, то сразу получим: у(х) = 2х2 - 12х + 14;
б) Теперь легко найти у(-2) = 2 · (-2)2 - 12 · (-2) + 14 = 8 + 24 + 14 = 46.
Пример 11
Известно, что ![]() Найдем х(у).
Найдем х(у).
Обозначим буквой z = x - 2, тогда х = z + 2, и запишем условие задачи: ![]() или
или ![]()
![]() To же условие запишем для аргумента (-z):
To же условие запишем для аргумента (-z): ![]() Для удобства введем новые переменные a = y(z) и b = y(-z). Для таких переменных получим систему линейных уравнений
Для удобства введем новые переменные a = y(z) и b = y(-z). Для таких переменных получим систему линейных уравнений
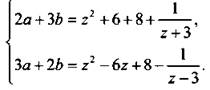
Нас интересует неизвестная a.
Для ее нахождения используем способ алгебраического сложения. Поэтому умножим первое уравнение на число (-2), второе уравнение - на число 3. Получим:
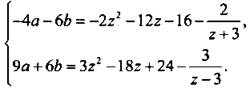
Сложим эти уравнения: ![]() откуда
откуда ![]()
![]() Так как аргумент функции можно обозначать любой буквой, то имеем:
Так как аргумент функции можно обозначать любой буквой, то имеем: ![]()
![]()
В заключение заметим, что к концу 9 класса были изучены свойства и графики:
а) линейной функции у = кх + m (график - прямая линия);
б) квадратичной функции у = ах2 + bх + с (график - парабола);
в) дробно-линейной функции ![]() (график - гипербола), в частности функции
(график - гипербола), в частности функции ![]()
г) степенной функции у = ха (в частности, функции ![]()
![]()
д) функции у = |х|.
Для дальнейшего изучения материала рекомендуем повторить свойства и графики указанных функций. На следующих занятиях будут рассмотрены основные способы преобразования графиков.
III. Контрольные вопросы
1. Дайте определение числовой функции.
2. Расскажите о способах задания функции.
3. Что называется объединением множеств А и B?
4. Какие функции называются целыми рациональными?
5. Какие функции называются дробно-рациональными? Как находится область определения таких функций?
6. Что называют графиком функции f(х)?
7. Приведите свойства и графики основных функций.
IV. Задание на уроках
§ 1, № 1 (а, г); 2 (в, г); 3 (а, б); 4 (в, г); 5 (а, б); 6 (в); 7 (а, б); 8 (в, г); 10 (a); 13 (в, г); 16 (а, б); 18.
V. Задание на дом
§ 1, № 1 (б, в); 2 (а, б); 3 (в, г); 4 (а, б); 5 (в, г); 6 (г); 7 (в, г); 8 (а, б); 10 (б); 13 (а, б); 16 (в, г); 19.
VI. Творческие задания
1. Найдите функцию у = f(х), если:
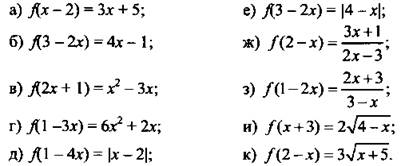
Ответы: ![]()
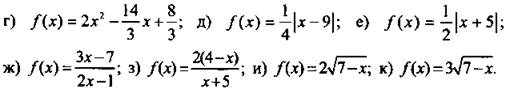
2. Найдите функцию у = f(x) если:
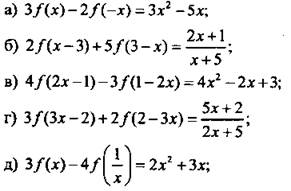
![]()
Ответы: ![]()

VII. Подведение итогов уроков