ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для рассмотрения признаков параллелограмма и закрепления полученных знаний в процессе решения задач

Термины и понятия

Параллелограмм, противолежащие стороны, противолежащие углы

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, какой многоугольник называется параллелограммом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии

Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи; понимают и используют наглядность для иллюстрации, интерпретации, аргументации.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); групповая (Г); индивидуальная (И)

Образовательные ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Актуализация опорных знаний

Цель деятельности

Деятельность учителя

Деятельность учащихся

Повторить основные элементы параллелограмма, его свойства и признаки

(Ф/И) 1. Дает задание подготовить у доски свойства параллелограмма с доказательством (для учащихся со слабым уровнем подготовки). (Выслушать индивидуально каждого отвечающего.)

(Ф/И) 2. Дает задание доказать самостоятельно следующие свойства параллелограмма (для учащихся с высоким уровнем подготовки):

1) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

2) Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой. (После подготовки выслушать доказательства дополнительных свойств параллелограмма.)

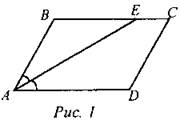
1) Дано: ∆BCD - параллелограмм, АЕ - биссектриса ∠BAD.

Доказать: ∆АВЕ - равнобедренный.

Доказательство: так как ABCD - параллелограмм, значит ВС || AD, тогда ∠EAD = ∠BEA,как накрест лежящие при параллельных прямых ВС и AD и секущей АЕ. АЕ - биссектриса ∠BAD, значит ∠BAE = ∠EAD,поэтому ∠BAE =∠BEA.

В ∆АВЕ ∠BAE = ∠BEA, значит, ∆АВЕ - равнобедренный с основанием АЕ.

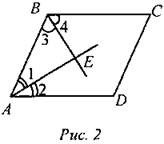
2а) Дано: ABCD - параллелограмм, BE - биссектриса ∠CBA, АЕ -биссектриса ∠BAD.Доказать: BE ⊥ AE.

Доказательство: АЕ - биссектриса, следовательно, ∠1 =∠2. BE - биссектриса => ∠3 = ∠4. В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, поэтому ∠ABC +∠BAD = 180°, то есть∠1 + ∠2 + ∠3 + ∠4 = 180°.

Так как ∠1 = ∠2, ∠3 = ∠4, то 2 ∙ (∠1 + ∠3)= 180°, ∠1 + ∠3 = 90°.

В ∆АВЕ ∠AEB = 180° -(∠1 + ∠3) = 90°, то есть BE ⊥ АЕ.

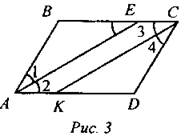
2б) Дано: ABCD - параллелограмм, АЕ, СК - биссектрисы ∠A= ∠C.

Доказать: АЕ || СК или АЕ и СК совпадают.

Доказательство: так как ABCD - параллелограмм, то∠2 = ∠BEA, как накрест лежащие при параллельных прямых ВС и AD и секущей АЕ.

В параллелограмме противолежащие углы равны, следовательно, ∠BAD= ∠BCD, значит, ∠1 =∠2 = ∠3 = ∠4. Так как ∠2 = ∠BEA, ∠2 =∠3, то ∠BEA = ∠3 => прямые АЕ и СК параллельны по признаку параллельности прямых. Прямые АЕ и СК совпадут, если в параллелограмме смежные стороны равны

Наводящие вопросы:

- Сформулируйте признак равнобедренного треугольника.

- Какие углы в ∆ВАЕ могут быть равными? Почему?

Наводящие вопросы:

- Когда прямые АЕ и СК будут параллельными?

- Равны ли ∠BEA и ∠3? Почему?

- В каком случае АЕ и СК совпадут?

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Создать условия для введения признаков параллелограмма

(Ф)

- Что означают слова “свойства” и “признак”? Приведите примеры.

- Какую теорему называют обратной?

- Всегда ли верно утверждение, обратное данному? Приведите примеры

III этап. Учебно-познавательная деятельность

Изучение нового материала

Цель деятельности

Совместная деятельность

Сформулировать признаки параллелограмма

(Ф)

- Сформулируйте утверждения, обратные свойствам параллелограмма. Всегда ли они верны?

(Г/Ф) Далее учащихся можно распределить на группы (по рядам) для учебно-исследовательской работы. Обсудить доказательства, сделать запись на доске и в тетради.

1. Если АВ = CD и АВ || CD, то ABCD - параллелограмм.

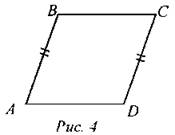
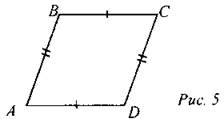
2. Если АВ = CD и ВС = AD, то ABCD - параллелограмм.

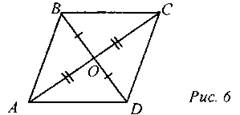
3. Если АС ∩ BD = О, АО = ОС и ВО = ОС, то ABCD - параллелограмм.

Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Закрепить полученные знания

(Ф/И) 1. Решите задачу № 379 (на доске и в тетради).

(И) 2. Решите задачу № 380 (самостоятельно)

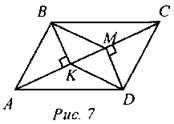
Дано: ABCD - параллелограмм, ВК ⊥АС, DM ⊥ АС.

Доказать: BMDK- параллелограмм.

Доказательство:

1) ∆ВКМ = ∆DMA по гипотенузе и острому углу (∠ВСК = ∠DAC,как накрест лежащие углы при параллельных прямыхAD и ВС и секущей АС, ВС = AD, как противолежащие стороны параллелограмма, ∆ВКС и ∆DMAпрямоугольные), значит MD = ВК.

2) ∆ВМК и ∆DKM -прямоугольные, ∆ВМК = ∆DKM по двум катетам (MD = ВК, КМ - общий катет), значит, ВМ = DK.

3) В четырехугольникеBMDKпротиволежащие стороны равны (MD =ВК и ВМ = DK),следовательно, BMDK– параллелограмм

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И) Если в задаче необходимо доказать, что ABCD - параллелограмм, то применяют один из признаков:

1. Если АВ - CD и АВ || CD, то ABCD - параллелограмм.

2. Если АВ = CD и ВС = AD, то ABCD - параллелограмм.

3. Если АС ∩ BD = О, АО = ОС и ВО = ОС, то ABCD - параллелограмм.

- На каком этапе урока у вас возникли трудности?

(И) Домашнее задание: выучить признаки параллелограмма; решить № 382, 383