Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПЛОЩАДЬ ТРАПЕЦИИ - ПЛОЩАДЬ
|
Цель деятельности учителя |
Создать условия для доказательства теоремы о площади трапеции |
||||
|
Термины и понятия |
Площадь треугольника, площадь трапеции |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют принимать решение в условиях неполной и избыточной, точной и вероятностной информации. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
||||
|
I этап. Проверка домашнего задания. Теоретический опрос |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Проверить уровень усвоения теоретических знаний; выявить трудности, возникшие при выполнении домашнего задания |
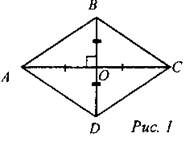
(Ф/И) Провести блицопрос по теории. К доске вызывается учащийся для решения домашнего номера № 476 (а). Остальные ученики задают вопросы, возникшие у них. Задача № 476 (а). Решение:
Диагонали ромба разбивают его на четыре равных прямоугольных треугольника => площади этих треугольников равны.
Так как диагонали ромба точкой пересечения делятся пополам, то
Ответ: 224 см2 |
||||
|
Решение задачи с целью подготовки учащихся к восприятию нового материала |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Посредством решения задачи подготовить учащихся к восприятию новой темы |
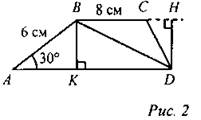
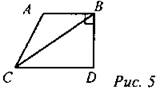
(И/Ф) Задача решается самостоятельно с последующим коллективным обсуждением решения. Найдите площадь трапеции ABCD, если основания AD и ВС равны соответственно 12 см и 8 см, боковая сторона АВ равна 6 см, ∠А = 30°. Решение:
Проведем высоту ВК в треугольнике ABD, которая равна высоте в треугольнике BCD, то есть ВК = DH.
BKDH - прямоугольник, поэтому ВК = DH, тогда Найдем ВК из прямоугольного треугольника АВК, в котором ∠A = 30°, АВ = 6 см;
Ответ: SABCD = 27 см2 |
||||
|
II этап. Изучение нового материала |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Доказать формулу для вычисления площади трапеции |
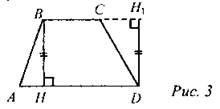
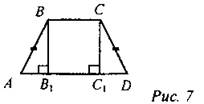
(Ф/Г) 1. Понятие высоты трапеции. Определение. Перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание, называют высотой трапеции. ВН, DH1 - высоты трапеции ABCD. ВН = DH1.
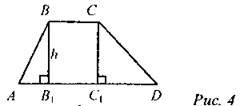
2. Решение задачи. Найти площадь трапеции ABCD, если основания AD и ВС равны а и b соответственно, а высота - Н. Задачу можно предложить решить самостоятельно или в небольших группах, затем обсудить решение, записать на доске и в тетрадях в виде теоремы с доказательством. Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту. (Теорема доказывается учителем вместе с учениками; можно предложить учащимся самостоятельно разобрать ее по учебнику.) |
||||
|
III этап. Решение задач на закрепление изученной формулы |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
На примерах простых задач отработать применение доказанной формулы |
(Ф/И) 1. Решить задачу. Дана трапеция, в которой основания равны 2 и 7, а площадь 18. Найти высоту. 2. Решить № 480, 481, 482 (самостоятельно в парах, с последующей проверкой) |
Ответ: высота равна 4. № 480.
а) Если АО = 21 см, СВ = 17 см, h = 7 см, то б) Если ∠D = 30°, ВС = 2 см, AD = 10 см, DC = 8 см, то S- ? В ∆DCC1 ∠C1 = 90°, ∠D = 30°, значит,
в) АВ = 5 см, ВС = 8 см, CD = 13 см, то
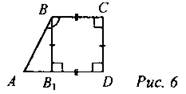
№ 481. Дано: ABCD - трапеция. ∠D = 90°, ВС = CD = 6, ∠B =135°. Найти: SABCD.
Решение: 1) ВВ1⊥ AD, рассмотрим ∆АВВ1: ∠B1 = 90°, ∠A = ∠B = 45°, значит, AB1 = BB1 = CD = 6 см, отсюда AD = АВ1 +B1D = 6 + 6 = 12 см. 2) Ответ: 54 см2. № 482. Дано: ABCD - трапеция. АВ = CD, ∠B = 135°. Найти: SABCD. Решение:
1) Рассмотрим ∆АВВ1: ∠B1 = 90°, ∠A = ∠B = 45°,следовательно, AB1 = BB1 = 1,4 см; аналогично из ∆CC1D: C1D = СС1 = 1,4 см. 2) B1C1 = B1D - C1D В1С1 = 3,4 - 1,4 = 2 см, значит, ВС = 2 см. AD = АВ1 + B1D = 1,4 + 3,4 = 4,8 см. 3) Ответ: 4,76 см2 |
|||
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Составьте синквейн к уроку |
(И) Домашнее задание: § 2, вопрос 7, с. 133; № 518 |
||||