РОМБ. КВАДРАТ - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для введения понятий ромба и квадрата как частных видов параллелограмма, для рассмотрения свойств и признаков ромба и квадрата; показать их применение в процессе решения задач

Термины и понятия

Ромб, квадрат, диагонали, углы

Планируемые результаты

Предметные умения

Универсальные учебные действия

У меют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в процессе решения задач.

Регулятивные: проявляют познавательный интерес к изучению предмета.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: умеют контролировать процесс и результат учебной математической деятельности

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для фронтальной, групповой работы

I этап. Проверка домашнего задания

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при выполнении домашнего задания

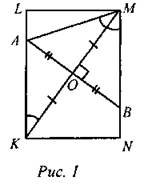
(Ф) 1. Дайте определение прямоугольника.

2. Перечислите свойства прямоугольника. Докажите одно из них.

3. Перечислите признаки прямоугольника.

4. Решите задачу:

Через середину диагонали КМ прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, пересекающая стороны KL и MN в точках А и В соответственно. Известно, что АВ = ВМ = 6. Найдите большую сторону прямоугольника.

а) Прямоугольные ∆МОВ и ∆КОА равны по катету и прилежащему к нему острому углу (КО = МО, так как О - середина диагонали КМ; ∠BMO = ∠AKO, как накрест лежащие при параллельных прямых KL и MN и секущей КМ), тогда АО = ОB = 3 см (АВ = 6 см), АК = МВ = 6 см.

б) ∆AMO = ∆ВМО по двум катетам (АО = ВО, МО - общая сторона, ∠AOM = ∠MOB = 90°), тогда АМ = МВ = 6 см и ∆АМВ - равносторонний.

в) ∠AMO = ∠BMO = 30°, так как ∆АМВ - равносторонний, МО - медиана, высота и биссектриса ∆АМВ.

г) ∠KLM = 90°, ∠AMO = 30°, ∠BMO = 30°, тогда ∠AML = 30°.

д) ∆ALM- прямоугольный, в нем ∠AML = 30°, АМ = 6 см, тогда AL = 3 см.

е) АК = 6 см, AL = 3 см, тогда КL = 9 см.

Ответ: KL = 9 см.

5. Решите задачи по готовым чертежам:

1) ABCD - прямоугольник. Найти: ∠ABF.

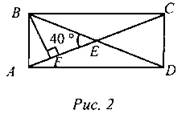
2) АСЕК - прямоугольник, ВС = 5 см. Найти: P_BDFM.

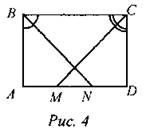
3) ABCD - прямоугольник. Доказать: АМ = ND.

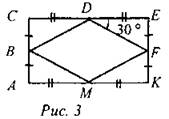
4) ABCD - прямоугольник. Найти: ∠AOB, ∠BOC.

5) ABCD - прямоугольник. Найти: АС, АВ.

6) ABCD - прямоугольник. Найти: AD.

II этап. Учебно-познавательная деятельность

Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятия ромба, квадрата, рассмотреть свойства и признаки этих фигур

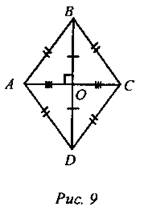
(Ф) 1. Введение понятия ромба.

Picture и записи на доске и в тетрадях учащихся:

ABCD - ромб, если ABCD - параллелограмм и АВ - ВС = CD = DA.

- Верно ли утверждение: “Четырехугольник, у которого все стороны равны, является ромбом”?

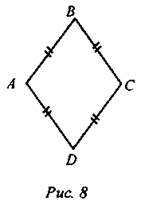
(Г/Ф) 2. Свойства ромба, признак ромба.

- Перечислите все свойства ромба как частного вида параллелограмма.

- Выясните, каким еще свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. (Работа в группах с последующим обсуждением свойства диагоналей ромба.)

На доске и в тетрадях записать:

Свойства ромба (рис. 9):

Если ABCD - ромб, то:

а) AB = BC = CD = AD;

б) АВ || CD, AD || ВС;

в) ∠A = ∠C, ∠B = ∠D;

г) АО = ОС, ВО = OD\

д) AC ⊥ BD.

е) АО, ВО, СО, DO - биссектрисы углов А, В, С, D.

(Г/Ф) - Сформулируйте утверждение, обратное особому свойству ромба, и выясните его справедливость.

(Работа в группах с последующим обсуждением.)

3. Определение квадрата.

ABCD - квадрат, если ABCD - прямоугольник, АВ = ВС = CD = DA.

- Верно ли утверждение: “Ромб, у которого все углы прямые, является квадратом”?

- Верно ли утверждение: “Параллелограмм, у которого все стороны и все углы равны, является квадратом”?

4. Свойства квадрата, признаки квадрата.

- Перечислите свойства квадрата, учитывая, что квадрат - это частный случай прямоугольника и ромба. Записать на доске и в тетрадях:

Свойства квадрата:

а) АВ = ВС = CD = AD; АВ || СD; ВС || AD;

б) ∠A = ∠B = ∠C = ∠D = 90°

в) ВО = ОС = OD = АО, BD ⊥ АС, АО, ВО, СО, DO - биссектрисы ∠A, ∠B, ∠C, ∠D соответственно.

- Сформулируйте признаки квадрата

Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Закрепить полученные знания

(Ф/И) 1. Решить задачу № 406.

(И) 2. Решить самостоятельно № 407

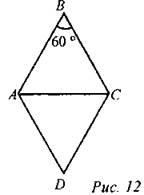
Дано: ABCD - ромб, ∠B = 60°, АС = 10,5 см.

Найти: Р_АВCD.

Решение:

∠B = 60°, АВ = ВС (так как АВ и ВС - стороны ромба), тогда ∠BAС = ∠BCA= 60°, то есть ∆АВС - равносторонний и АВ = АС = 10,5 см. У ромба все стороны равны, поэтому P_ABCD = 4 ∙ АВ = 4 ∙ 10,5 = 42 (см).

Ответ: 42 см.

Решение:

∠ABC = 45°.

BD - диагональ и биссектриса ∠ABC.

∠ABD = 45° : 2 = 22°30'

Из ∆ABO (∠O = 90°, так как диагонали ромба перпендикулярны):

∠OAB = 90° - 22°30' = 67°30'

Ответ: 22°30’, 67°30'

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали на уроке?

- Какой этап урока оказался для вас самым сложным?

- Оцените свою работу на уроке

(И) Домашнее задание: п. 47 прочитать; решить № 412, 413