Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Свойства действий над числами - ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
Цель: напомнить основные свойства сложения и умножения.
Планируемые результаты: усвоить основные свойства действий над числами.
Тип урока: урок изучения нового материала.
Ход урока
I. Сообщение темы и цели урока
II. Работа по теме урока
Напомним основные свойства операций сложения и умножения чисел.
1. Переместительное свойство: a + b = b + a и a ∙ b = b ∙ а (для любых чисел а и b). От перестановки слагаемых сумма чисел не меняется. От перестановки множителей произведение чисел не меняется.
Пример 1
На основании переместительного свойства выполняются равенства:

Разумеется, это свойство справедливо не только для двух чисел, но и для любого количества слагаемых или множителей.
Пример 2
На основании переместительного свойства выполняются равенства:
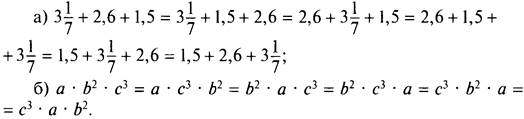
2. Сочетательное свойство: (а + b) + с = а + (b + с) и а ∙ (b ∙ с) = (а ∙ b) ∙ с (для любых чисел а, b и с).
При сложении или умножении чисел их можно произвольным образом объединить в группы.
Пример 3
На основании сочетательного свойства выполняются равенства:
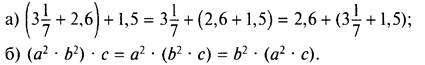
Это свойство также справедливо для любого количества чисел. Переместительное и сочетательное свойства часто используются для наиболее рационального сложения или умножения чисел.
Пример 4
Вычислим наиболее рациональным способом:
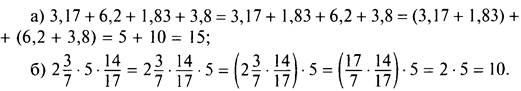
3. Распределительное свойство: а ∙ (b + с) = a ∙ b + a ∙ с (для любых чисел а, b и с). При умножении числа на сумму чисел данный множитель умножается на каждое слагаемое и полученные произведения складываются.
Пример 5
На основании распределительного свойства выполняются равенства:
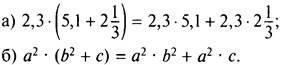
Распределительное свойство справедливо и в том случае, когда в сумму входит любое число слагаемых.
Пример 6
Справедливо равенство ![]()
Распределительное свойство также используется для рациональных вычислений выражений.
Пример 7
Вычислим рациональным способом:
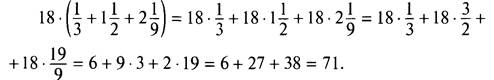
Заметим, что операцию вычитания можно заменить операцией сложения, прибавив к уменьшаемому число, противоположное вычитаемому, т. е. а - b = а + (-b). Поэтому вычитание можно считать алгебраической суммой чисел. Разумеется, переместительное, сочетательное и распределительное свойства справедливы и в этом случае.
Пример 8
Используя переместительное, сочетательное и распределительное свойства, вычислим:
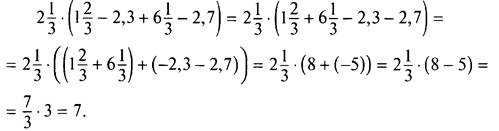
III. Задания на уроке
№ 70 (а, в), 71 (а, в), 72 (а, г), 73 (а), 74 (а), 75 (а, г), 76 (а, в), 77 (а), 78 (а), 79 (а).
IV. Контрольные вопросы
— Запишите формулировки основных свойств сложения и умножения.
— Дайте словесную формулировку свойств сложения и умножения.
— Для каких чисел справедливы основные свойства сложения и умножения?
V. Творческие задания
1. Проверьте равенства:

Какие свойства сложения и умножения при этом использовали?
2. Вычислите наиболее рациональным способом:
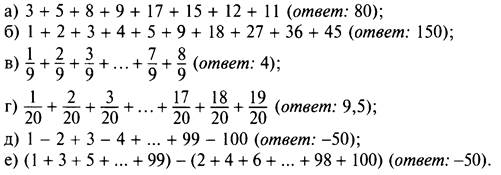
VI. Подведение итогов урока
Домашнее задание
№ 70 (б, г), 71 (б, г), 72 (б, в), 73 (б), 74 (б), 75 (б, в), 76 (б, г), 77 (б), 78 (б), 79 (б).