Зачет по теме Системы линейных уравнений - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Цели: сравнить успеваемость учащихся при одинаковой сложности заданий; иметь возможность повысить оценки за выполненные контрольные работы.

Тип уроков: уроки контроля, оценки и коррекции знаний.

Ход уроков

I. Сообщение темы и целей уроков

II. Общая характеристика зачетной работы

Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи представлены в блоке А, более сложные — в блоке В, еще сложнее — в блоке С. Каждая задача из блока А оценивается 1 баллом, из блока В — 2 баллами, из блока С — 3 баллами. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка “3” ставится за 6 баллов, оценка “4” — за 10 баллов, оценка “5” — за 14 баллов.

Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Работа рассчитана на два урока.

III. Зачетная работа

Вариант 1

А

1. Графическим способом решите систему уравнений

2. Способом подстановки решите систему уравнений

3. Способом сложения решите систему уравнений

4. Парабола у = ах² + b проходит через точки A (2; 5) и B (4; 11). Найдите числа а и b.

5. Используя графический способ, определите число решении системы уравнений

6. При всех значениях параметра а определите число решений системы уравнений

7. На стоянке 18 машин и велосипедов, у которых вместе 60 колес. Сколько машин и сколько велосипедов находится на стоянке?

В

8. Способом подстановки решите систему уравнений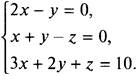

9. При каких значениях параметра а система уравнений не имеет решений?

10. Решите уравнение 2х² - 2х + 4у² + 4ху + 1 = 0.

11. Напишите уравнение ломаной, изображенной на рисунке.

C

12. Пусть (x₀; у₀; z₀) — решение системы уравнений 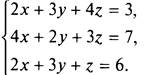Найдите сумму x₀ + у₀ + z₀.

13. Сколько лет брату и сестре, если 4 года назад брат был старше сестры в 5 раз, а через 5 лет брат будет старше сестры в 2 раза?

14. Напишите уравнение прямой, проходящей через точку А (2; 3) и через точку пересечения графиков функций у = |х| и у = |х - 2|.

Вариант 2

А

1. Графическим способом решите систему уравнений

2. Способом подстановки решите систему уравнений

3. Способом сложения решите систему уравнений

4. Парабола у = ах² + b проходит через точки А (1; 3) и В (3; -5). Найдите числа а и b.

5. Используя графический способ, определите число решении системы уравнений

6. При всех значениях параметра а определите число решений системы уравнений

7. На стоянке 26 машин и велосипедов, у которых вместе 88 колес. Сколько машин и сколько велосипедов находится на стоянке?

В

8. Способом подстановки решите систему уравнений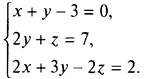

9. При каких значениях параметра а система уравнений не имеет решений?

10. Решите уравнение х² + 10у² - 6ху + 4у + 4 = 0.

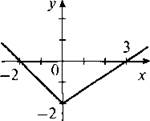
11. Напишите уравнение ломаной, изображенной на рисунке.

С

12. Пусть (x₀; у₀; z₀) — решение системы уравнений 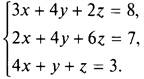Найдите сумму x₀ + у₀ + z₀.

13. Сколько лет брату и сестре, если 3 года назад брат был старше сестры в 4 раза, а через 5 лет брат будет старше сестры в 2 раза?

14. Напишите уравнение прямой, проходящей через точку А (1; 5) и через точку пересечения графиков функций у = |х + 2| и у = |х|.

IV. Разбор задач (ответы и решения)

Вариант 1

А

1. (1; -1).

2. (2; 1).

3. (-1; 3).

4. a = 0,5, b = 3.

5. Два решения.

6. При а ≠ 1,5 единственное решение, при a = 1,5 решений нет.

7. 12 машин, 6 велосипедов.

В

8. (1; 2; 3).

9. При а ≠ ±2.

10. (1; -1/2).

11.

C

12. В системе уравнений в левые части каждая из переменных входит ровно 8 раз. Поэтому сложим левые и правые части всех трех уравнений. Получаем 2х + 3у + 4z + 4x + 2y + 3z + 2x + 3y + z = 3 + 7 + 6, или 8х + 8у + 8z = 16, или 8(х + у + z) = 16.

Разделим обе части этого равенства на число 8 и найдем х + у + z = 2. Поэтому если (х₀; у₀; z₀) — решение данной системы, то х₀ + у₀ + z₀ = 2.

(Ответ: 2.)

13. Пусть сейчас брату х лет, сестре у лет. Брату 4 года назад было х - 4 лет, а сестре у - 4 лет. По условию брат был старше сестры в 5 раз. Поэтому получаем уравнение х - 4 = 5(у - 4). Через 5 лет брату будет х + 5 лет, а сестре у + 5 лет. Тогда брат будет в 2 раза старше сестры. Имеем второе уравнение х + 5 = 2(у + 5).

Получили систему уравнении или

Так как в уравнениях одинаковые левые части, то приравняем и правые. Получаем линейное уравнение с одним неизвестным: 5у - 16 = 2у + 5 или 3у = 21, откуда у = 7. Из первого уравнения находим х = 5 ∙ 7 - 16 = 35 - 16 = 19. Итак, сейчас брату 19 лет, а сестре 7 лет.

(Ответ: брату 19 лет, сестре 7 лет.)

14. Сначала найдем точку пересечения графиков функций у = |х| и у = |х - 2|. Для этого построим графики таких функций (графики I и II соответственно). Видно, что графики пересекаются в одной точке В (1; 1).

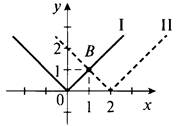
Теперь рассмотрим линейную функцию у = ах + b. По условию ее график проходит через точки А (2; 3) и В (1; 1). Поэтому координаты этих точек удовлетворяют уравнению линейной функции. Получаем систему уравнении

Решим эту систему способом подстановки. Из второго уравнения выразим а = 1 - b. Подставим это значение в первое уравнение и получим 3 = 2(1 - b) + b, или 3 = 2 - 2b + b, или 1 = -b, откуда b = -1. Используя формулу а = 1 - b, найдем а = 1 - (-1) = 2. Итак, уравнение данной прямой у = 2х - 1.

(Ответ: у = 2х - 1.)

Вариант 2

А

1. (2; 1).

2. (1; -1).

3. (2; -1).

4. а = -1, b = 4.

5. Два решения.

6. При а ≠ 1,5 единственное решение, при а = 1,5 решений нет.

7. 18 машин, 8 велосипедов.

В

8. (1; 2; 3).

9. При а ≠ ±2.

10. (-6; -2).

11.

12. В системе уравнений 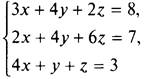в левые части каждая из переменных входит ровно 9 раз. Поэтому сложим левые и правые части всех трех уравнений. Получаем 3х + 4у + 2z + 2х + 4у + 6z + 4х + у + z = 8 + 7 + 3, или 9х + 9у + 9z = 18, или 9(х + у + z) = 18.

Разделим обе части этого равенства на число 9 и найдем х + у + z = 2. Поэтому если (x₀; у₀; z₀) — решение данной системы, то х₀ + у₀ + z₀ = 2.

(Ответ: 2.)

13. Пусть сейчас брату х лет, а сестре у лет. Брату 3 года назад было x - 3 лет, а сестре у - 3 лет. По условию брат был старше сестры в 4 раза. Поэтому получаем уравнение x - 3 = 4(у - 3). Через 5 лет брату будет х + 5 лет, а сестре у + 5 лет. Тогда брат будет в 2 раза старше сестры. Имеем второе уравнение х + 5 = 2(у + 5).

Получили систему уравнении или

Так как в уравнениях одинаковые левые части, то приравняем и правые. Получаем линейное уравнение с одним неизвестным: 4у - 9 = 2у + 5 или 2у - 14, откуда у = 7. Из первого уравнения находим х = 4 ∙ 7 – 9 = 28 – 9 = 19. Итак, сейчас брату 19 лет, а сестре 7 лет.

(Ответ: брату 19 лет, сестре 7 лет.)

14. Сначала найдем точку пересечения графиков функций у = |х + 2| и у = |х|. Для этого построим графики таких функций (графики I и II соответственно). Видно, что графики пересекаются в одной точке В (-1; 1).

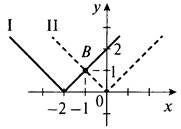
Теперь рассмотрим линейную функцию у = ах + Ь. По условию ее график проходит через точки А (1; 5) и В (-1; 1). Поэтому координаты этих точек удовлетворяют уравнению линейной функции. Получаем систему уравнений

Решим эту систему способом сложения. Сложим левые и правые части уравнений системы и получим 5 + 1 = b + b или 6 = 2b, откуда b = 3. Подставим это значение в первое уравнение системы 5 = a + 3, откуда a = 2. Итак, уравнение данной прямой у = 2х + 3. (Ответ: у = 2х + 3.)

V. Подведение итогов уроков