Способ подстановки - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: рассмотреть способ подстановки для решения систем линейных уравнений.

Планируемые результаты: научиться применять способ подстановки для решения систем линейных уравнений.

Тип уроков: урок изучения нового материала, продуктивный урок.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

I. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Что называется решением системы уравнений с двумя переменными?

2. Запишите условие единственности решения системы уравнений.

3. Графически решите систему уравнений

4. При каких значениях параметра а система уравнений несовместна?

Вариант 2

1. Что значит решить систему уравнений?

2. Запишите условие несовместности системы уравнений.

3. Графически решите систему уравнений

4. При каких значениях параметра а система уравнений имеет единственное решение?

III. Работа по теме уроков

Системы уравнений с двумя переменными, которые имеют одни и те же решения или не имеют решений, называются равносильными.

Пример 1

а) Две системы уравнений равносильны, так как имеют одно и то же решение (2; 1).

б) Две системы уравнений равносильны, так как каждая из них не имеет решений.

При решении системы уравнений с помощью преобразований ее заменяют более простой равносильной системой. Одним из распространенных способов решения систем уравнений является способ подстановки. Рассмотрим его на примере.

Пример 2

Решим систему уравнений

Из первого уравнения выразим переменную у через х и получим у = 4 - 2х (заметим, что данное уравнение равносильно исходному). Подставим это выражение во второе уравнение вместо переменной у и получим систему

Докажем, что системы (1) и (2) равносильны.

В системе (2) второе уравнение содержит только одну переменную х. Решим это линейное уравнение. Получаем 3х - 8 + 4х = -1 или 7х = 7, откуда х = 1. Подставим значение х = 1 в первое уравнение системы (2) и найдем у = 4 - 2 ∙ 1 = 2. Пара чисел (1; 2) — решение системы (2), а значит, и системы (1).

В равносильности систем (1) и (2) легко убедиться. Решение х = 1, у = 2 является единственным решением системы (2). В системе (1) коэффициенты при неизвестных удовлетворяют условию Поэтому она имеет единственное решение. Подставив значения х = 1, у = 2 в эту систему, убеждаемся, что такая пара чисел и есть решение системы (1).

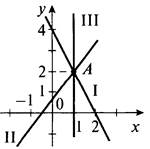
Также можно убедиться в равносильности систем (1) и (2), используя графический способ. Для этого нужно показать, что графики уравнений системы (1) пересекаются в той же точке, что и графики уравнений системы (2). Сначала построим график первого уравнения системы (1) — прямую I, затем график второго уравнения — прямую II. Они пересекаются в точке А.

Графиком первого уравнения системы (2) является прямая I. График второго уравнения — вертикальная прямая х = 1 (прямая III). Видно, что эти графики также пересекаются в точке А. Поэтому системы (1) и (2) равносильны.

Система линейных уравнений с двумя переменными была решена способом подстановки. Заметим, что таким способом решаются и системы нелинейных уравнений.

При решении систем этим способом:

1) выражают из какого-нибудь уравнения системы одну переменную через другую;

2) подставляют в другое уравнение полученное выражение вместо этой переменной;

3) решают полученное уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

Пример 3

Решим систему уравнений

Выразим из первого уравнения переменную у через х. Получаем 4у = 5 - 3х или

Подставим во второе уравнение вместо у полученное выражение Получаем уравнение с одной переменной: Умножим все члены уравнения на число 4. Получаем 8х - 5(5 - 3х) = 12, или 8х - 25 + 15х = 12, или 23х = 37, откуда

Подставим в уравнение вместо х число 37/23 и получим

Итак, единственное решение данной системы

Заметим, что найти это решение графическим способом можно лишь приближенно.

Способом подстановки можно решать и системы уравнений, содержащих параметры.

Пример 4

При каких значениях параметра а решением системы уравнений будет неотрицательная пара чисел?

Из первого уравнения выразим переменную у = 2х + 3 и подставим ее во второе уравнение. Получаем 3х + 2(2х + 3) = 7a - 1, или 3х + 4х + 6 = 7a - 1, или 7х = 7а - 7.

Разделим все части равенства на число 7 и найдем х = а - 1. Используя выражение у = 2х + 3, находим у = 2(а - 1) + 3 = 2а - 2 + 3 = 2а + 1. При каждом значении параметра а система уравнений имеет единственное решение х = а - 1 и у = 2а + 1. По условию такие числа должны быть неотрицательны. Число х = а - 1 неотрицательно при значениях а, не меньших числа 1 (т. е. а ≥ 1). При таких значениях а число у = 2а + 1 будет положительным. Итак, а ≥ 1.

IV. Задания на уроках

№ 1068 (а), 1069 (а, в, д), 1070, 1073, 1075, 1077 (а, б), 1078 (а, в).

V. Контрольные вопросы

— Какие системы уравнений называются равносильными?

— Как решить систему уравнений способом подстановки?

VI. Творческие задания

1. Решите систему уравнений:

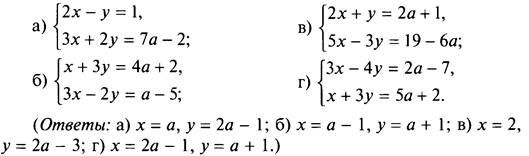
2. При каком значении параметра а решение (х₀; у₀) системы уравнений удовлетворяет условию?

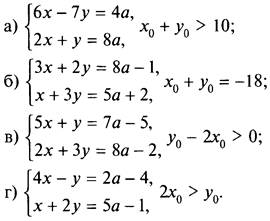
(Ответы: а) а > 2 (решение х₀ = 3а, у₀ = 2а); б) а = -6 (решение х₀ = 2а - 1, у₀ = а + 1); в) при всех а (решение x₀ = а - 1, у₀ = 2а); г) нет таких значений а (решение х₀ = а - 1, у₀ = 2а).)

VII. Подведение итогов уроков

Домашнее задание

№ 1068 (б), 1069 (б, г, е), 1071, 1074, 1076, 1077 (в, г), 1078 (б, г).