Разложение на множители с помощью формул квадрата суммы и квадрата разности - КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ

Цель: научить раскладывать выражения на множители с помощью формул квадрата суммы и квадрата разности.

Планируемые результаты: научиться раскладывать выражения на множители, выделять полный квадрат суммы или разности. Тип уроков: уроки изучения нового материала.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Напишите формулу куба суммы двух чисел (выражений).

2. Преобразуйте в многочлен выражение (а - 2)³.

3. Упростите выражение (х + 1)³ + (х - 1)³.

Вариант 2

1. Напишите формулу куба разности двух чисел (выражений).

2. Преобразуйте в многочлен выражение (а + 3)³.

3. Упростите выражение (х + 1)³ - (х - 1)³.

III. Работа по теме уроков

Формулы квадрата суммы и квадрата разности используют для разложения на множители многочленов вида а² + 2ab + b² и а² - 2ab + b², выделения полных квадратов суммы и разности чисел, доказательства тождеств, неравенств и т. д. Запишем формулы, рассмотренные на предыдущем уроке, поменяв местами левую и правую части: а² + 2ab + b² - (а + b)² и а² - 2ab + b² = (а - b)².

Заметим, что выражение с² = с ∙ с. Поэтому приведенные формулы можно рассматривать как разложение многочлена на множители. Представление выражения а² + 2ab + b² в виде (а + Ь)² и выражения а² - 2ab + b² в виде (а - b)² называют также выделением полных квадратов суммы и разности.

Пример 1

Разложим на множители многочлен 4х² + 12х + 9. Первое слагаемое 4х² представляет собой квадрат выражения 2х, третье — квадрат числа 3. Легко проверить, что второе слагаемое — удвоенное произведение выражения 2х и числа 3, т. е. 12х- = 2 ∙ 2х ∙ 3. Тогда данный многочлен имеет вид 4х² + 12х + 9 = (2х)² + 2 ∙ 2х ∙ 3 + 3² = (2х + 3)².

Пример 2

Разложим на множители выражение 9а² - 30ab² + 25b⁴. Первое слагаемое 9а² является квадратом выражения 3а, третье слагаемое 25b⁴ — квадратом выражения 5b². Легко проверить, что второе слагаемое — удвоенное произведение выражений 3а и 5b², т. е. 30ab² = 2 ∙ 3а ∙ 5b². Тогда данный трехчлен имеет вид

Пример 3

Найдем наименьшее значение выражения A = 2а² - 4а + 10.

В данном выражении вынесем общий множитель 2 за скобки: А = 2(а² - 2а + 5).

В выражении а² - 2а + 5 выделим полный квадрат разности:

Поэтому данное выражение можно записать в виде А = 2((а - 1)² + 4) = 2 (а - 1)² + 8.

Очевидно, что слагаемое 2(а - 1)² ≥ 0. Выражение А будет принимать наименьшее значение, если слагаемое 2(а - 1)² будет наименьшим, т. е. 2(а - 1)² = 0. Уравнение выполняется, если а - 1 = 0, т. е. а = 1. Тогда наименьшее значение данного выражения

Пример 4

Докажем, что при всех значениях переменных а и b значение выражения больше 1.

В данное выражение А входят две переменные а и b. Представим слагаемое 2а² в виде 2а² = а² + а² и сгруппируем члены выражения:

Выражение в скобках является квадратом разности а - Ь. Чтобы в оставшихся слагаемых выделить квадрат суммы, представим число 6 в виде суммы чисел 6 = 4 + 2. Тогда выражение А имеет вид

При всех значениях переменных an b выражения (а - b)² ≥ 0 и (а + 2)² ≥ 0, поэтому данное выражение А ≥ 2 и тем более А > 1.

IV. Задания на уроках

№ 833 (а, б), 835 (б, в), 836 (а, в), 837, 839 (а, б), 842 (а), 844 (г, д), 848 (а, в).

V. Творческие задания

1. Найдите наименьшее (или наибольшее) значение выражения. При каком(их) значении(ях) переменной(ых) оно достигается?

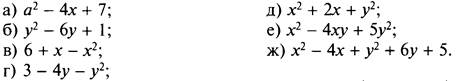
(Ответы: а) 3 при х = 2; б) -8 при у = 3; в) при х = 1/2; г) 7 при у = -2; д) -1 при x = -1, у = 0; е) 0 при х = у = 0; ж) -8 при х = 2, y = -3.

2. Докажите неравенство:

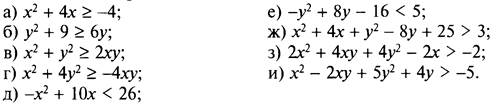
VI. Подведение итогов уроков

Домашнее задание

№ 833 (в, д), 835 (а, д), 836 (б, г), 838, 839 (г, д), 842 (б), 844 (а, б), 848 (б, г).