Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Понятие о графике уравнения - ЛИНЕЙНАЯ ФУНКЦИЯ - ФУНКЦИИ
Цель: рассмотреть графики уравнений.
Планируемые результаты: научиться строить графики простейших уравнений.
Тип урока: урок-исследование.
Ход урока
I. Сообщение темы и цели урока
II. Работа по теме урока
До сих пор мы рассматривали только функциональные зависимости (функции). В таких зависимостях каждому значению переменной х соответствовало только одно значение переменной у. В математике встречаются и такие зависимости между переменными х и у, при которых одному значению х может соответствовать не одно, а множество значений у. Множество точек (х; у), связанных такой зависимостью, можно изобразить на координатной плоскости. В этом случае говорят о графике уравнения.
Пример 1
На координатной плоскости изобразите множество таких точек (х; у), которые удовлетворяют уравнению х = 3.
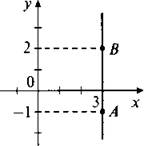
Видно, что в уравнение х = 3 переменная у не входит. Поэтому любое значение у будет удовлетворять данному уравнению. Возьмем, например, точки А (3; -1) и В (3; 2). Координаты этих точек удовлетворяют уравнению, поэтому такие точки принадлежат искомому графику. Через точки А и В проведем прямую линию. Эта прямая параллельна оси ординат и является графиком уравнения х = 3.
Заметим, что раньше мы строили графики функций у = а (где а — некоторое число) и получали прямые, параллельные оси абсцисс. Поэтому построенный график аналогичен рассмотренным раньше.
Отметим, что этот график является именно графиком уравнения (а не функции), так как одному значению переменной х соответствует бесконечно много значений переменной у.
Пример 2
На координатной плоскости изобразите множество таких точек (х; у), которые удовлетворяют уравнению (у - 1)(у - х) = 0.
Сначала из данного уравнения найдем величину у. Если произведение двух множителей равно нулю, то либо первый множитель равен нулю, либо второй. Поэтому рассмотрим два случая:
1) у - 1 =0, отсюда у = 1. Построим эту прямую, параллельную оси абсцисс;
2) у - х = 0, отсюда у = х. Построим график этой прямой пропорциональной зависимости (биссектриса первого и третьего координатных углов).
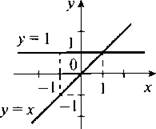
Две пересекающиеся прямые у = 1 и у = х и являются графиками данного уравнения. Разумеется, построенный график является именно графиком уравнения, а не графиком функции. Например, как видно на рисунке, одному значению х = -1 соответствуют два различных значения у: у = -1 и у = 1.
Пример 3
Построим график уравнения (2х - 1)(2х + 4) = 0.
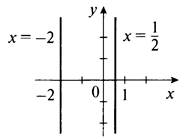
Так как произведение двух множителей равно нулю, то один из множителей должен равняться нулю. Получаем 2х - 1 = 0 (откуда х = 1/2) и 2х + 4 = 0 (откуда х = -2). Построим две прямые х = 1/2 и х = -2, параллельные оси ординат, и получим график данного уравнения.
Пример 4
Построим график уравнения |у| = х.
Для этого раскроем в уравнении модуль, рассмотрев два случая. Если у ≥ 0, то уравнение имеет вид у = х. Построим прямо пропорциональную зависимость у = х и выберем такие точки на этой прямой, для которых ордината у ≥ 0 (сплошная прямая).
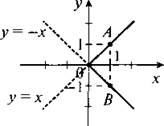
Если у < 0, то уравнение имеет вид -у = х или у = -х. Построим график данной зависимости. Выберем на этой прямой такие точки, для которых ордината у < 0 (сплошная прямая).
Таким образом, графиком данного уравнения будет ломаная AОВ.
Пример 5
Построим график уравнения у = х ∙ |у|.
Сначала найдем более простую связь между переменными х и у. Запишем уравнение в виде 0 = х ∙ |у| - у и раскроем знак модуля, рассмотрев два случая:
1. Если у ≥ 0, то уравнение имеет вид 0 = у(х - 1). Это уравнение выполняется, если у = 0 или x = 1. Величина у = 0 удовлетворяет условию у ≥ 0. Построим эту прямую (ось абсцисс).

Из графика зависимости x = 1 выберем такие точки, для которых ордината у ≥ 0.
2) Если у < 0, то уравнение имеет вид 0 = -ху - у. Так как у ≠ 0, то разделим все члены уравнения на у и получим 0 = -х - 1, откуда х = -1. Построим эту прямую x = -1 и из графика выберем такие точки, для которых ордината у < 0.
Таким образом, график данного уравнения состоит из оси абсцисс (у = 0) и двух лучей x = 1 и x = -1. Отметим, что при рассмотрении уравнения и его графика понятия области определения и области значений не вводятся (в отличие от функции). В старших классах будет продолжено изучение графиков уравнений, а также будут рассмотрены графики неравенств.
III. Задания на уроке и на дом
Постройте на координатной плоскости множество точек (х; у), для которых выполняется равенство:
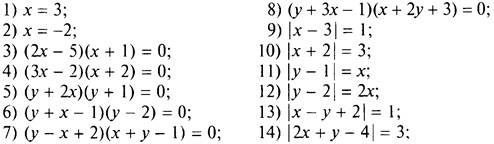
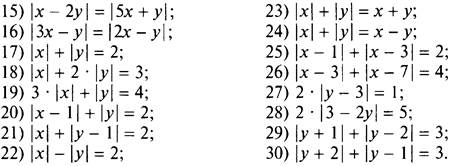
IV. Подведение итогов урока